《概率论与数理统计》课程教学资源（PPT课件）3.5 两个随机变量函数的分布

复习：一维连续型随机变量的函数的分布 问题：已知X的密度fx(x),求Y=g(X)的密度f(Oy) 方法1 F,(y)=P{Y≤}=P{g(X)≤y} =∫sfx(dx,(-o0(<0), x=(Uy)是g(x)的反函数，a<y<B(是y=g(x)的有效值域) (a,)=)且1田≠0)-

复习：一维连续型随机变量的函数的分布 ( ) { } { ( ) } F y P Y y P g X y Y =  =  ( ) ( )d , ( ), X g x y f x x x  = −     方法1 方法2 [ ( )] ( ) , , ( ) 0, . X Y f h y h y y f y       =   其它 ( ) ( ) ( ) 问题：已知X f x Y g X f y 的密度 X Y ，求 = 的密度 [ ( ) ] ( ) F y f y Y y Y  = ( ) ( ) 0( 0), ( ) ( ) , ( ( ) ) y g x g x x h y g x y y g x   =    =   = 处处可导，且恒有 是 的反函数 是 的有效值域 ( , ( ) ( ) 0 )= y y g x f x =  且 

第五节 两个随机变量函数的分布 (一)Z=X+Y的分布 (-yZ=及Z=X灯的分布 X (三)M=max(X,Y)及N=min(X,Y)的分布

第五节 两个随机变量函数的分布 Y Z Z XY X = = （二）* 及 的分布 （一）Z X Y = + 的分布 （三）M X Y N X Y = = max( , ) min( , ) 及 的分布

(一)Z=X+Y的分布 本节重点 设(X,Y)的概率密度为f(x,y),则Z=X+Y 的分布函数为 Fza)=P{Z≤=PX+r≤z=∬fx,y)dxdy &’-[xa x+y≤ Le-g∫[a-a]ay Ax+y=z =∫[fu-ar小a 由此可得：fa)=∫fz-y,dy

设( , ) ( , ), X Y f x y Z X Y 的概率密度为 则 = + 的分布函数为 ( , )d d x y z f x y x y +  =  x y O x y z + = ( , )d d z y f x y x y  − − −   =       x u y = − ( , )d d z f u y y u y  − −   −       由此可得： （一）Z X Y = + 的分布 —— 本节重点 ( ) { } F z P Z z Z =  = +  P X Y z { }  x z y u z = − = ( , )d d . z f u y y y u  − −   = −       f z f z y y y Z ( ) ( , )d  − = − 

za)=∫mfz-y)dy 同理可得：z2)=fx,z-x)dx XY独立时，f2a)=∫人(a-O)dy fa)=J」f(x)f(&-x)dx 这两个公式称为∫x和f,的卷积公式，记为x*,即： f*f=J」人xa-yf)dy=∫」fx(xf,-dx 5:e=f(,)dxdy主了f.(f(ydxdy x+y≤z x+y≤2

X, Y 独立时, f f f z y f y y X Y X Y * ( ) ( )d  − = −  ( ) ( )d . X Y f x f z x x  − = −  f z f x z x x Z ( ) ( , )d  − = −  f z f z y y y Z ( ) ( , )d  − = −  f z f z y f y y Z X Y ( ) ( ) ( )d  − = −  f z f x f z x x Z X Y ( ) ( ) ( )d  − = −  同理可得： 这两个公式称为 X Y f f X Y 和 的 卷积公式, 记为 f f  ，即： ( , )d d x y z f x y x y +   ( ) F z Z = X Y, 独立 X Y ( ) ( )d d x y z f x f y x y +  

例1.设两个独立的随机变量X与Y都服从标准正态分布， 求Z=X+Y的概率密度。 解：因f田=1e号 =e2,-0<x<0 f0-2 e 2,-oo<p<00, 阳-f-ar-0e,号a: 2π 1e, =√π 即Z服从N(0,2)分布。 2√π

1. X Y Z X Y = + 例 设两个独立的随机变量 与 都服从标准正态分布， 求 的概率密度。 解： 因 2 2 1 ( ) , 2 x X f x e x  − = −     2 2 1 ( ) , , 2 y Y f y e y  − = −     2 z 2 2 t x = − 1 4 2 d 2 z z x e e x    −  − −     − =  2 2 4 1 d 2 z t e e t  −  − − 2 4 1 , 2 z e  − = f z f x f z x x Z X Y ( ) ( ) ( )d  − = −  2 2 ( ) 2 2 1 d 2 x z x e e x  −  − − − =  即Z N 服从 （0 2，）分布。 = 

说明： (1)若X,Y相互独立且X~N(41,o),Y~N(42,o),则 X+Y~N(41+42,G1+G2) (2)若X:~N(,o)(i=1,2,.,m)且它们相互独立，则 空xN空42 (3)有限个相互独立的正态随机变量的线性组合仍然服从正态 分布.如(1)中的X,Y,有 X+bY~N(a41+b42,a2o1+b2o2)

（3）有限个相互独立的正态随机变量的线性组合仍然服从正态 分布. 如(1) , 中的X Y，有 2 2 1 1 1 2 ~ ( , ) ( 1,2, , ) ~ ( , ) i i i n n n i i i i i i X N μ σ i n X N μ σ = = = =    （ ）若 且它们相互独立，则 说明： 2 2 1 1 2 2 2 2 1 2 1 2 1 , ~ ( , ), ~ ( , ) ~ ( , ). X Y X N μ σ Y N μ σ X Y N + + + μ μ σ σ （ ）若 相互独立且 ，则 2 2 2 2 1 2 1 2 aX bY N a + + + ~ ( , ) μ bμ a σ b σ

例2.在一简单电路中，两电阻卫1和几2串联联接，设R1,R2 相互独立，它们的概率密度均为 10-x 0≤x≤10， f(x)= 50 0, 其它 求电阻R=R+R,的概率密度. x=10 ,x=z-10 解 由题意知R的概率密度为 fn(a)=∫fxfk-x)dx 0 被积函数不为零的区域： ∫0<x<10, 0即12-0<x<a 0<x<10, 0<z-x<1

1 2 1 2 1 2 , 10 , 0 10, ( ) 50 0, . R R R R x x f x R R R  −    =    = + 在一简单电路中，两电阻 和 串联联接，设 相互独立，它们的概率密度均为 其它 求电阻 的概率密度. 解 由题意知 R的概率密度为 例2. 0 10, 0 10, x z x       −  0 10, . 10 , x z x z      −   即 O 10 20 z x x = z x = z − 10 x = 10 被积函数不为零的区域： ( ) ( ) ( )d . R f z f x f z x x  − = − 

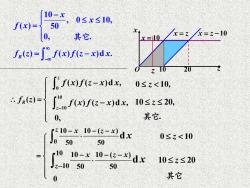
10-x f(x)= 50 0≤x≤10， 0,其它 x=10 x=z=2-10 f(a)=J」fx)fz-x)dx. 7 2 f(x)f(z-x)dx, 0≤z<10, /2-)dx,10≤z≤20， 0, 其它 “5ax 0≤z<10 50 r1010-x.10-(z-dx J2-050 10≤z≤20 50 其它

O 10 20 z x x = z x = z − 10 x = 10 10 , 0 10, ( ) 50 0, . x x f x      −   = 其它 ( ) R f z     =     0 ( ) ( )d , z f x f z x x −  10 10 ( ) ( )d , z f x f z x x − −  0, 0 10,  z 10 20,  z 其它. z    =     10 10 10 10 ( ) 50 50 d z x z x x − − − −   10 20  z 0 10 10 ( ) 50 50 d z x z x x − − −   0 10  z 0 其它 ( ) ( ) ( )d . R f z f x f z x x  − = − 

600z-60z2+z)/15000,0≤z0 Jx(x)=04I(a) a>0,0>0, 0 其它 0=a2TAei>0 1 B>0,0>0, (0 其它 试证明Z=X+Y~T(a+B,0)。 注：「函数

2 3 3 (600 60 ) 15000, 0 10, ( ) (20 ) 15000, 10 20, 0, . R z z z z f z z z  − +    = −       其它 1 1 0 ( ) , ( ) 0 x α X x e x f x α    − −    =     其它 α   0, 0,  1 1 0 ( ) , ( ) 0 y Y y e y f y      − −    =     其它 β   0, 0,  例 3 设随机变量 X、Y 相互独立且X ~ ( , )  α  ，Y ~ ( , )  β  ， 其概率密度分别为 试证明Z X Y = +  + ~ ( , )    。 注：Γ函数

推广：若X,~「(a,)(i=1,2,m)且它们相互独立，则 x+x+x)

推广：若 ~ ( , ) Xi i    ( 1, 2, , ) i n = 且它们相 互独 立， 则 1 2 1 ~ ( , ) n n i i X X X   = + + +  