山东理工大学：《线性代数》课程教学课件（PPT讲稿）第四章 线性方程组 第三节 非齐次线性方程组

⑨本理子大军 第三节非齐次线性方程组 一非齐次线性方程组解的性质 二应用举例 三小结 上页 返回

©中东理王大 、 非齐次线性方程组解的性质 1、非齐次线性方程组 anx+ax2+L+aux=b azx+ax2+L+azx=b (1) LLLLLLLLLL Iam+am22+Lamnxnbm 2e011 L12 L eb,1 z 422 L 若记A=S L Cansr=e L .b-c C M C M edm L 8x 则上述方程组 (1)可写成向量方程 A.x

１、非齐次线性方程组 若记 （1） 一、非齐次线性方程组解的性质 则上述方程组（1）可写成向量方程

©本理工大 又可记xa,+x42+L+x0m=b. (2) 非齐次方程组Ax=b对应的齐次方程组Ax=0 称为该非齐次方程组的导出组. 2、非齐次线性方程组解的性质 (1)若x,=h1,x2=h为Ax=b的解，则x=h1-h2 是对应的齐次方程组Ax=0的解 (2)若x=x为Ax=0的解，x=h为Ax=b的解， 则x=x+h也是Ax=b的解 (3) 若h2,山h,都为c=b的解，则，+h,+L+h 也是Ar=b的解

（2）若 为 的解， 为 的解， 又可记 ２、非齐次线性方程组解的性质 （1）若 为 的解，则 是对应的齐次方程组 的解. （２） 非齐次方程组 称为该非齐次方程组的导出组. 则 也是 的解． 也是 的解． （3）若 都为 的解，则 对应的齐次方程组

©中东理大 3、非齐次线性方程组的通解 非齐次线性方程组Ax=b的通解为 x=kx+kx2Lkh. 其中k,+kx2+L+knxm,为其导出组的通解， h 为非齐次线性方程组的任意一个特解 L、 非齐次线性方程组有解的几个等价命题 王王王王王 线性方程组Ax=有解，则以下命题等价： 向量b可由向量组a1,a2L,a,线性表示 向量组a1,a2,L,0n与向量组a1,02,L,4n,b等价 R(aa2L,a)=R(aa2L,ab)

其中 为其导出组的通解， ３、非齐次线性方程组的通解 非齐次线性方程组 的通解为 为非齐次线性方程组的任意一个特解. ４、非齐次线性方程组有解的几个等价命题 线性方程组 有解，则以下命题等价： 向量ｂ可由向量组 线性表示. 向量组 与向量组 等价

⑤山本理工大罗 二、 应用举例 例1 求解下列非齐次线性方程组 ìx1-2x2+2x3-x4=1 12x1-4x2+8x3=2 i-2x1+4x2-2x3+34=3 13x1-6x2-6x4=4 解 方程组的增广矩阵为 ael -2 2 -1 1 l-22-1 -4 8 0 2 0 2 0 B=C S-2 4-2 3 3÷ 0 83-6 0 -6 0 QR(A)1R(B),所以线性方程组无解 回

例１ 求解下列非齐次线性方程组 二、应用举例 解 方程组的增广矩阵为 所以线性方程组无解

2 求解下列非齐次线性方程组 东理工大 ix+x2-3x3-x4=1 3x-x-3s+4-4 1x+5x-9x,-8x=0 方程组的增广矩阵为 ael 1-3-116 ael 1 -3 -1 1 B= 93 -1 -3 4 0 -4 6 7 5 -9 -8 0店 4 -6 -7 ÷0 -1 d 1 -3 -1 16 ael 1 -3 0 S -4 6 7 3 1 0 2 0 0 0 0

例２ 求解下列非齐次线性方程组 解 方程组的增广矩阵为

⑤中本理子大军 0 3 5 0 -2 4 4 80 3 1 2 74 4÷ 0 0 0 因R(A)=R(B)=3<4,所以线性方程组有无穷多解 3 3 对应的方程组为： 3 2 3 上页 回

因 所以线性方程组有无穷多解. 对应的方程组为:

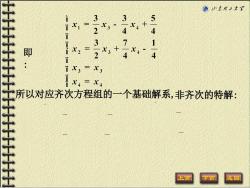
©中东理王大 3 3 5 2 i 3 7 1 即 4 4 i 所以对应齐次方程组的一个基础解系，非齐次的特解：

即 : 所以对应齐次方程组的一个基础解系,非齐次的特解:

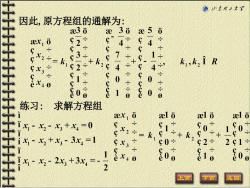
©少本理工大军 因此，原方程组的通解为： ae3 0 2e10 89 3-4 ÷ 5-4 S 2 k1 3 > 1-4 k,k21 R 0 ÷÷÷÷÷ 0 1 0 练习： 求解方程组 0 ael 6 ael 6 ael o 1x-x2-x+x4=0 ÷ 2÷=k 91 1 9 0 ix-x2+3-3x4=1 k2 S0÷ 2÷ 21 ￥-2+3x=- 8x 81 0 2 上页 回

因此,原方程组的通解为: 练习: 求解方程组

©出东理子大军 例2 求解下列非齐次线性方程组 ì2x1-x2-x3+x4=2 ix+2-2x+x=4 i4x-6x,+2x3-2x=4 13x+6x2-9x+7x=9 解 方程组的增广矩阵为 a2 -1-1 126 el0-10 46 1-2 1 4 01-1 0 3 B=S S4-6 2-24÷ς00 ,3÷ 3 6-9 79g800 00 因R(A)=R(B)=3<4,所以线性方程组有无穷多解 上页 下顶

因 所以线性方程组有无穷多解. 例２ 求解下列非齐次线性方程组 解 方程组的增广矩阵为