《概率论与数理统计》课程教学资源（PPT课件）3.4 相互独立的随机变量

第四节相互独立的随机变量 一、两个随机变量的相互独立性 二、n个随机变量的相互独立性

一、两个随机变量的相互独立性 二、 n 个随机变量的相互独立性 第四节 相互独立的随机变量

一、两个随机变量的相互独立性 定义设F(x,y)及Fx(x),F(y)分别是二维随机变量(X,Y) 的分布函数及边缘分布函数。若对于所有x,y有 P{X≤x,Y≤y}=P{X≤x}P{Y≤y, 即 F(x,y)=Fx(x)Fy(y), 则称随机变量X与Y是相互独立的。 X与Y相互独立 一对任意x,y,随机事件{X≤x}与{Y≤y}相互独立. 台对任意x,y,随机事件{X>x}与{Y>y}相互独立

一、两个随机变量的相互独立性 定 义 设 ( , ) ( ), ( ) F x y F x F y 及 X Y 分别是二维随机变量（X，Y） 的分布函数及边缘分布函数。若对于所有 x, y 有 P X x Y y P X x P Y y { , } { } { },   =   即 ( , ) ( ) ( ), F x y F x F y = X Y 则 称随机变量 X 与 Y 是相互独立的。    对任意 x y X x Y y , ，随机事件 与 相互独立． X Y 与 相互独立    对任意 x y X x Y y , ，随机事件 与 相互独立．

1.若(X,Y)为离散型随机变量 X与Y相互独立台P{X=x,Y=y}=P{X=x}P{Y=y} oPi=P。P 2.若（X,Y)为连续型随机变量 X与Y相互独立台f(x,y)=fx(x)fr(y) 在全平面上几乎处处成立

{ , } { } { }  = = = = = P X x Y y P X x P Y y i j i j 1. 若（X，Y ）为离散型随机变量 ij i j p p p  =  • • X Y 与 相互独立 2. 若（X，Y ）为连续型随机变量 ( , ) ( ) ( ) X Y  = f x y f x f y 在全平面上几乎处处成立。 X Y 与 相互独立

例如： X 1 2 3 P.j 1 1-6 19 18 3 13 号 5 Pi. 2 3 石 可以验证， Pi PiP.j (i=1,2,3;j=1,2) →X与Y相互独立 补充定理X和Y相互独立，∫，g是连续函数， 则f(X)和g(Y)也相互独立

例如： X Y 1 2 3 1111 1 6 9 18 3 1 2 1 2 2 3 9 9 3 111 2 3 6 j i p p ij i j p p p 可以验证， =   (i j = = 1, 2, 3 1, 2 ； )  X Y 与 相互独立． 补充定理 X Y f g 和 相互独立, , 是连续函数， 则 f X g Y ( ) ( ) . 和 也相互独立

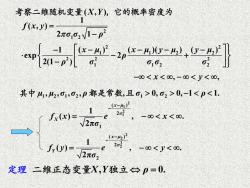
考察二维随机变量(X,Y),它的概率密度为 f,0产2o,-p 即g 0102 -000,02>0，-1<p<1. _(x-4)2 1“,-w<x<o fx(x=2π _(x-2 f(y)2no: 2,-0<y<0. 定理二维正态变量X,Y独立→p=0

考察二维随机变量( , ) X Y ，它的概率密度为 −    −     x y , , 1 2 1 2 1 2 其中 μ , , , , , 0, 0, 1 1. μ σ σ ρ都是常数 且 σ   −   σ ρ 2 1 2 2 2 1 1 2 2 2 2 2 1 1 2 2 1 ( , ) 2 1 1 ( ) ( )( ) ( ) exp 2 2(1 ) f x y σ σ ρ x μ x μ y μ y μ ρ ρ σ σ σ σ  = −     −   − − − −  − +         −   2 2 2 2 ( ) 2 2 1 ( ) , . 2π x μ σ Y f y e y σ − − = −     2 1 2 1 ( ) 2 1 1 ( ) , . 2π x μ σ X f x e x σ − − = −     定理 二维正态变量X Y, 0. 独立  = ρ

例.一负责人到达办公室的时间均匀分布在8一12 时，他的秘书到达办公室的时间均匀分布在7~9时， 设他们两人到达的时间相互独立，求他们到达办 公室的时间相差不超过5分钟(1/12小时)的概率 解设X和Y分别是负责人和他的秘书到达办公室的时间， 由假设X和Y的概率密度分别为 V4,x [1/2,7<y<9, 0,其它， f0)=10, 其它， 由于X,Y相互独立，f(x,y)=fx()fr(y) 1/8,8<x<12,7<y<9, 0,其它

解 设 X Y 和 分别是负责人和他的秘书到达办公室的时间, 例. 一负责人到达办公室的时间均匀分布在8~12 时,他的秘书到达办公室的时间均匀分布在7~9时, 设他们两人到达的时间相互独立, 求他们到达办 公室的时间相差不超过 5 分钟（1/12小时）的概率. 由假设 X Y 和 的概率密度分别为 1 4, 8 12, ( ) 0, , X x f x    =   其它 由于 X Y, , 相互独立 ( , ) ( ) ( ) X Y f x y f x f y = 1 8, 8 12,7 9, 0, .      x y =   其它 1 2, 7 9, ( ) 0, , Y y f y    =   其它

-/n-27” 其他 PX-Y≤1/12 9 =∬fc,dxdy x-y=12 11 12 7- =8×(G的面积). 0 8 12

1 8, 8 12,7 9, 0,      x y =   其他 P X Y { 1 12} − ( , )d d G = f x y x y 1 ( ). 8 =  G 的面积 ( , ) ( ) ( ) X Y f x y f x f y = O x y 8 • 12 • 7 9 A C C B G B 1 12 x y − = 1 12 x y − = −

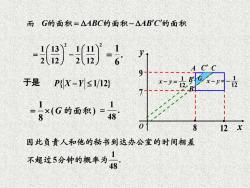
而G的面积=△ABC的面积-△AB'C的面积 旷=8 9- 于是 PX-Y≤1/12} 12 7 =8×(G的面积)= 48 0 8 12 因此负责人和他的秘书到达办公室的时间相差 不超过5分钟的概率为 48

2 2 1 13 1 11 2 12 2 12     = −         . 6 1 = 于是 P X Y { 1 12} −  1 ( ) 8 =  G的面积 1 . 48 = 1 5 . 48 因此负责人和他的秘书到达办公室的时间相差 不超过 分钟的概率为 而 G ABC AB C 的面积 =  −  的面积  的面积 O x y 8 • 12 • 7 9 A C C B G B 1 12 x y − = 1 12 x y − = −

二、n维随机变量的相关概念 1.分布函数n维随机变量(X1,X2,.,Xn)的分布函数 F(x1,x2,.,xn)=P{X1≤x1,X2≤x2,.,Xn≤xn}, 其中，x2,.,xn为任意实数. 2.概率密度函数 若存在非负函数f(x1,x2,.,x),使对于任意 实数1，X2,.,xn有 F()fddxd 则称f(x1,x2,xn)为(X1,X2,.,Xn)的概率密度函数

1. 分布函数 二、n 维随机变量的相关概念 2. 概率密度函数 1 1 1 2 1 2 1 2 ( , , , ) ( , , , )d d d , n n x x x F x x x f x x x x x x n n n − − − − =    1 2 1 2 ( , , , ) ( ) , , , . n n 则称 f x x x 为 X X X 的概率密度函数 1 2 1 1 2 2 ( , , , ) { , , , }, F x x x P X x X x X x n n n =    1 2 , , , . n 其中 x x x 为任意实数 1 2 ( , , , ) n X X X 维随机变量 n 的分布函数 1 2 1 2 ( , , , ), , , , n n f x x x x x x 若存在非负函数 使对于任意 实数 有

3.边缘分布函数 n维随机变量(X1,X2,Xn)关于X1的边缘分布函数 FX(x1)=F(x1,o,0,0o) (X1,X2,.,X)关于(X,X2)的边缘分布函数 FX1,x2(c1,x2)=F(x1,x2,o,o,.,o) 其它依次类推

1 2 1 ( , , , ) n X X X X 维随机变量 n 关于 的边缘分布函数. 其它依次类推. 3. 边缘分布函数 1 1 1 ( ) ( , , , , ) F x F x X =    1 2 1 2 ( , , , ) ( , ) X X X X X n 关于 的边缘分布函数. 1 2 , 1 2 1 2 ( , ) ( , , , , , ) F x x F x x X X =   