《概率论与数理统计》课程教学资源（PPT课件）2.3 随机变量的分布函数

第三节 随机变量的分布函数 ●分布函数的概念 ●分布函数的性质 ●求分布函数； ●用概率分布计算有关事件的概率

⚫ 分布函数的概念 ⚫ 分布函数的性质 ⚫ 求分布函数; 第三节 随机变量的分布函数 ⚫ 用概率分布计算有关事件的概率

一、引入 对于离散型随机变量利用分布律描述 P{X=x}=P,k=1,2,. PXeg=∑PX=x=∑p 对于非离散型随机变量：P{X=x。}=0(待证) 关心：P{x1<X≤x}=? P{x<X≤x}=P{X≤x,}-P{X≤x} 引入P{X≤x}=F(x)

一、引入 对于离散型随机变量 → 利用分布律描述 对于非离散型随机变量： { } , 1,2,. P X x p k = = = k k { } { } k k k k x L x L P X L P X x p    = = =   关心：P x X x  1 2   = ? P x X x  1 2    =  P X x  2 −  P X x  1 引入 P X x    = F x( )0 P X x { } 0 = = （待证）

二、分布函数的概念 定义设X是一个随机变量，x是任意实数，函数 F(x)=P{X≤x 称为X的分布函数 说明： ()分布函数F(x)是x的普通实函数， 定义域(-∞，o;对应法则：F(x)=P{X≤x} (2)Fx)反映随机变量取值X≤x的概率，故又称累计概率 函数。 (3)用Fx)可以表示随机变量X在任一区间1，x]的概率 完整描述了统计规律性

( ) { } . , , F x x P X x X X =  定义 设 是一个随机变量 是任意实数 函 称为 的分布函数 二、分布函数的概念 说明： (2) F(x)反映随机变量取值X ≤ x的概率，故又称累计概率 函数. (1) ( ) ( ) : ( ) { } F x x −   F x P X x =  分布函数 是 的普 定义 对 通实函数， 域 ， ； 应法则 (3) 用F(x)可以表示随机变量X在任一区间(x1 , x2 ] 的概率 ——完整描述了统计规律性

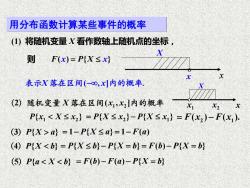
用分布函数计算某些事件的概率 ()将随机变量X看作数轴上随机点的坐标， X 则F(x)=P{X≤x 表示X落在区间(-oo,x内的概率. (2)随机变量X落在区间(x1,2]内的概率 P{x1a}=1-P{X≤a}=1-F(a) (4)P(X<B)=P(X<D)-P(X=b)=F(D)-P(X=b) (5)P{a<X<b}=F(b)-F(a)-P{X=b}

(1) 将随机变量 X 看作数轴上随机点的坐标， x x X o 1 2 P x X x { }   2 1 =  −  P X x P X x { } { } 2 1 = − F x F x ( ) ( ). 表示X x 落在区间( , ] − 内的概率. F P ( ) { } x =  X x 1 2 （2 ( , ] ）随机变量 X x x 落在区间 内的概率 用分布函数计算某些事件的概率 则 （3 { } ）P X a  = −  = − 1 { } 1 ( ) P X a F a x X o 1 x 2 x （5 { } ）P a X b   = − − = F b F a P X b ( ) ( ) { } （4 { } ）P X b  =  − = = − = P X b P X b F b P X b { } { } ( ) { }

三、分布函数的性质 (1)F(x)是一个单调不减函数， 证明：设x1<x2,有F(x)-F(x2) =P{X≤x2}-P{X≤x} =P{x1<X≤x2}≥0，→Fx)≤F(x2)

证明：设 1 2 x x  ，有 1 2 F x F x ( ) ( ) − 2 1 =  −  P X x P X x { } { } 1 2 =   P x X x { }  0, 1 2   F x F x ( ) ( ) （1 ( ) ）F x 是一个单调不减函数. 三、分布函数的性质

(2)0≤F(x)≤1，且 F(-oo)=lim F(x)=0 F(co)=lim F(x)=1. 分析： F(x)=P{X≤x},当x越来越小时， {X≤x}趋于不可能事件因而当x>-0时，有 limF(x)=IimP{X≤x}=0 七0 'x 同理 lim F(x)=lim PX00 (③)F(x)处处右连续。（证略) lim F(x)=F(xo),(oox<oo). x→x0

F x P X x ( ) { }, =  lim ( ) lim { } 0 x x F x P X x →− →− =  = o x 分析： 当 x 越来越小时, 因而当 x → −时,有 lim ( ) lim { } 1. x x F x P X x →  →  同理 =  = { } X x  趋于不可能事件 ( ) lim ( ) 1. x F F x →   = = （2 0 ( ) 1 ）   F x ，且 ( ) lim ( ) 0 x F F x →− − = = （3 ( ) ）F x 处处右连续。（证略） 0 0 0 lim ( ) ( ), ( ). x x F x F x x → + = −    x x

题型：“离散型随机变量分布律与分布函数的关系” 分布律 P4=P{X=x},k=1,2,. 可列可加性 分布函数F(x)=PX≤x=∑PX=x}=∑P:(x∈R) xhS.x YRSx 例1.设随机变量X的分布律为 X -1 2 3 Pk a 1-4 (1)求0；(2)X的分布函数； 3米Px≤P<X≤.P2sxs3

分布函数 F x P X x ( ) { } =  分布律 { }, 1, 2, . . k k p P X x k = = = 题型：“离散型随机变量分布律与分布函数的关系” ( x∈R ) 可列可加性 设随机变量 X 的分布律为 X pk −1 2 3 1 1 4 4  例1. (1) (2) 1 3 5 (3) { }, { }, {2 3}. 2 2 2 X P X P X P X       求 ； 的分布函数； 求 { } k k k k x x x x P X x p   = = =  

解(1)由分布律性质：1/4+a+1/4=1, 0=1/2 X|-123 固定模式 Pk 0, x<-1,） P{X=-1}, 1sx<2 (2)F(x)=P{X≤x= PX=-1y+PX=2,l2≤x<3 1, ≥3. 0, x<-1, 1F(x) 1/4, -1≤x<2, 即F(x)= 3/4, 2≤x<3, 1, x≥3. 0 23

k X p 解 （1）由分布律性质： 1/ 4 1/ 4 1, + + =   = 1 2/ 固定模式 x  −1, −   1 2, x 2 3,   x x  3. (2) ( ) F x P X x { }    =  =    0, P X{ 1}, = − P X P X { 1} { 2}, = − + = 1, 即 0, 1, 1 4, 1 2, ( ) 3 4, 2 3, 1, 3. x x F x x x   −   −   =        o x F(x) 1 -1 2 3 111 4 2 4 −1 2 3

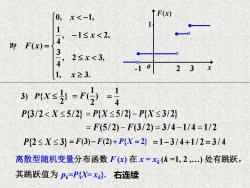
「0，x<-1, TF(x) 即F(x)= 4 -1≤x<2, 4 2≤x<3, 1,x≥3. 23 3)PX5F(- P{3/2<X≤5/2}=P{X≤5/2}-P{X≤3/2} =F(5/2)-F3/2)=3/4-1/4=1/2 P{2≤X≤3}=F3)-F(2)+PX=2=1-3/4+1/2=3/4 离散型随机变量分布函数Fx)在x=x4(k=1,2,)处有跳跃， 其跳跃值为PwPX=x}.右连续

1 3) { } 2 P X  P{3/ 2  X  5/ 2} = P{X  5/ 2}− P{X  3/ 2} = F(5/ 2) − F(3/ 2) = 3/ 4 −1/ 4 = 1/ 2 0, 1, 1 , 1 2, 4 ( ) 3 , 2 3, 4 1, 3. x x F x x x   −   −    =         即 1 ( ) 2 = F P{2  X  3} = − F F (3) (2) + P X{ 2} = 1 4 = = − + = 1 3 / 4 1 / 2 3 / 4 离散型随机变量分布函数 F (x) 在 x = xk (k =1, 2 ,.) 处有跳跃， 其跳跃值为 pk=P{X= xk }. o x F(x) 1 -1 2 3 右连续

例2：一个靶子是半径为2米的圆盘，设击中靶上任一同心圆盘上 的点的概率与该圆盘的面积成正比，并设射击都能中靶，以X表 示弹着点与圆心的距离.试求随机变量X的分布函数. 解1)x<0时，F(x)=P{X≤x}=0; 2)0≤x≤2时， F(x)=P{X≤x}=P{X<O}+P0≤X≤x} =P{0≤X≤x}=x2,k是常数.取x=2, 由P0≤X≤2=山，得h=l,→k=}F9= 4 3)当x≥2时，F(x)=P{X≤x} X≤x是必然事件 =P{X≤2}+P{2<X≤x}=1

例2：一个靶子是半径为2米的圆盘，设击中靶上任一同心圆盘上 的点的概率与该圆盘的面积成正比, 并设射击都能中靶, 以X 表 示弹着点与圆心的距离. 试求随机变量 X 的分布函数. 解 1) 0 , x  时 2) 0 2 ,   x 时 2 =   = P X x kx k {0 } , . 是常数 由P X {0 2} 1,   = 得 4 1, k = 1 . 4  = k F x P X x ( ) { } 0; =  = 2 ( ) 4 x  = F x F x P X x ( ) { } =  =  P X{ 0} +   P X x {0 } 取 x =2， 3) 2 , 当 x  时 F x P X x ( ) { } =  =  +   P X P X x { 2} {2 } = 1. X x  是必然事件