《概率论与数理统计》课程教学资源（PPT课件）2.1 随机变量

第二章随机变量及其分布 第一节随机变量 一、随机变量的引入 二、随机变量的概念 重点：随机变量的概念

二、随机变量的概念 一、随机变量的引入 第二章 随机变量及其分布 第一节 随机变量 重点：随机变量的概念

一、随机变量(random variable)的引入 一将形形色色的样本空间S中的元素e与实数x对应 起来，从而可用微积分方法研究。 问题：若记样本空间S={e}(e表示样本空间的元素)， 如何寻找一个规则X,将S的每个元素与实数x对应起来。 即 e∈S,e规则x→xeR 记作：X=X(e)随机变量

——将形形色色的样本空间 S 中的元素 e 与实数 x 对应 起来，从而可用微积分方法研究。 一、随机变量(random variable)的引入 若记样本空间 （ 表示样本空间的元素）， 如何寻找一个规则 ，将 的每个元素 与实数 对应起来 即 问题： { } . S e e X S e x =  e S, 记作：X X e = ( ) 规则 X e x R ⎯⎯⎯→  —— 随机变量

例1.将一枚硬币抛掷3次，以X表示出现H的总次数， 分析：数据如下表： 样本点HHH HHT HTH HTT THH THT TTH TTT X的值 2212110 X可能取的值为0,1,2,3. 3 e=HHH 2 e=HHT,HTH,THH ∴.X=X(e)= 1 e=HTT,THT,TTH e=TTT

分析：数据如下表： X的值 样本点 HHH HHT HTH HTT THH THT TTH TTT 3 2 2 1 2 1 1 0 X 可能取的值为 0，1，2，3.  = X X e( ) 3 2 , , 1 , , 0 e HHH e HHT HTH THH e HTT THT TTH e TTT  =  = =   = 例1. 将一枚硬币抛掷3次，以X H 表示出现 的总次数

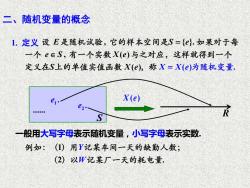
二、随机变量的概念 1.定义设E是随机试验，它的样本空间是S={}以.如果对于每 一个e∈S,有一个实数X(e)与之对应，这样就得到一个 定义在S上的单值实值函数X(e),称X=X(e)为随机变量. X(e) e2 S 一般用大写字母表示随机变量，小写字母表示实数. 例如：()用Y记某车间一天的缺勤人数； (2)以W记某厂一天的耗电量

, { }. , ( ) ( ) X X e( ) . E S e e S X e S X e =  = 设 是随机试验 它的样本空间是 如果对于每 一个 有一个实数 与之对应，这样就得到一个 定义在 上的单值实值函数 ，称 为随机变量 二、随机变量的概念 1. 定义 S X e( ) R . 2 e . 1 e . 例如：（ ）用 记某车间一天的缺勤人数； （ ）以 记某厂一天的耗电量 1 2 . Y W 一般用大写字母表示随机变量，小写字母表示实数

2.用随机变量表示事件及事件的概率 如例1.将一枚硬币抛掷3次，以X表示出现H的总次数， 3 e HHH 2 e=HHT,HTH,THH X=X(e)={ 1 e-HTT,THT,TTH 0 e-TTT (X=2)A-(HHT,HTH,THH),P(X=2)=P(A)= 3 P(Xs1-P(HTT,THT.TTH,TTT)-7 一般地，设L是一个实数集，则 {x∈L}=事件B-{elx(e)eL} P{X∈L}=P(B)=P{eIX(e)∈L}

2. 用随机变量表示事件及事件的概率 X X e = ( ) 3 2 , , 1 , , 0 e HHH e HHT HTH THH e HTT THT TTH e TTT  =   = =  =    = { 2} X =  A HHT HTH THH = { , , }, 3 ( ) 8 P X{ 2} = = = P A 一般地，设L是一个实数集，则 X L   = 事件B e X e L =   | ( )  P X L    = =  P B P e X e L ( ) | ( )   如例1. 将一枚硬币抛掷3次，以X H 表示出现 的总次数. X  = 1 HTT THT TTH TTT ,  1 2 P P =

3.说明：随机变量与普通的函数不同 (1)普通函数是定义在实数轴上的，而随机变量是定义 在样本空间上的（样本空间的元素不一定是实数） (2)随机变量的取值具有一定的概率规律 随机变量随着试验的结果不同而取不同的值，由于试验的 各个结果的出现具有一定的概率，因此随机变量的取值也有一 定的概率规律

（1）普通函数是定义在实数轴上的，而随机变量是定义 在样本空间上的(样本空间的元素不一定是实数). 3. 说明：随机变量与普通的函数不同 （2）随机变量的取值具有一定的概率规律 随机变量随着试验的结果不同而取不同的值, 由于试验的 各个结果的出现具有一定的概率, 因此随机变量的取值也有一 定的概率规律

例.某公共汽车站每隔5分钟有一辆汽车通过，如果某人 到达该车站的时刻是随机的，则 X(e)="此人的等车时间"， X(e)所有可能取值为：I0,5] 例.设某射手每次射击打中目标的概率是0.8，现该射手 不断向目标射击，直到击中目标为止，则 X(e)="所需射击次数"， 且X()的所有可能取值为：1,2,3

例. 设某射手每次射击打中目标的概率是0.8，现该射手 不断向目标射击，直到击中目标为止,则 例. 某公共汽车站每隔5 分钟有一辆汽车通过, 如果某人 到达该车站的时刻是随机的, 则 X e( ) " ", = 此 人 的 等 车 时 间 X(e) 所有可能取值为: [0,5]. X e( ) " ", = 所 需 射 击 次 数 且 X(e) 的所有可能取值为: 1, 2, 3,

4.随机变量的分类 随机变量 离散型 非离散型 连续型 其它 (1)离散型 随机变量所取的可能值是有限多个或无限多 个（可列个），叫做离散型随机变量. (2)连续型【 随机变量所取的可能值可以连续地充满某个 区间叫做连续型随机变量

4. 随机变量的分类 离散型 (1)离散型 随机变量所取的可能值是有限多个或无限多 个(可列个), 叫做离散型随机变量. 随机变量 连续型 非离散型 其它 (2)连续型 随机变量所取的可能值可以连续地充满某个 区间,叫做连续型随机变量