《概率论与数理统计》课程教学资源（PPT课件）6.1 随机样本

数理统计是具有广泛应用的一个数学分支，它以概率论 为理论基础，根据试验或观察得到的数据，来研究随机现象， 对研究对象的客观规律性作出种种合理的假设和判断。 概率论所研究的随机变量，它的分布都是假设已知的，在 这一前提下去研究它的性质、特点和规律性。 数理统计所研究的随机变量，它的分布是未知的，通过对 随机变量进行重复独立的观察，得到许多观察值，对这些数据 进行分析，对随机变量作出种种推断

数理统计是具有广泛应用的一个数学分支，它以概率论 为理论基础，根据试验或观察得到的数据，来研究随机现象， 对研究对象的客观规律性作出种种合理的假设和判断。 概率论所研究的随机变量，它的分布都是假设已知的，在 这一前提下去研究它的性质、特点和规律性。 数理统计所研究的随机变量，它的分布是未知的，通过对 随机变量进行重复独立的观察，得到许多观察值，对这些数据 进行分析，对随机变量作出种种推断

描述统计学一如何收集、整理数据资料 数理统计 对随机现象进行观测、试验，以取得有 代表性的观测值.抽样 推断统计学一如何分析数据 分类 如何对已取得的观测值进行分析、研究，作 出推断、决策，从而找出所研究的对象的规 律性。 只介绍统计推断的基本内容

对随机现象进行观测、试验，以取得有 代表性的观测值.——抽样 如何对已取得的观测值进行分析、研究，作 出推断、决策，从而找出所研究的对象的规 律性. 数 理 统 计 的 分 类 描述统计学——如何收集、整理数据资料 推断统计学——如何分析数据 只介绍统计推断的基本内容

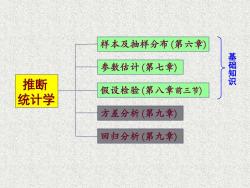
样本及抽样分布（第六章） 参数估计（第七章） 基础知识 推断 假设检验（第八章前三节） 统计学 方差分析（第九章） 回归分析（第九章）

参数估计 (第七章) 假设检验 (第八 章前三节) 回归分析 (第九章) 方差分析 (第九章) 推断 统计学 基础知识 样本及抽样分布 (第六章 )

第六章样本及抽样分布 本章主要内容： (1)总体、样本、统计量等基本概念； (2)三个抽样分布及四个重要定理。 一一一一一一一一一

第六章 样本及抽样分布 本章主要内容： （1）总体、样本、统计量等基本概念； （2）三个抽样分布及四个重要定理

第一节随机样本一基本概念 一、总体与个体 二、简单随机样本

二、简单随机样本 第一节 随机样本——基本概念 一、总体与个体

一、总体与个体 研究有关对象的某一数量指标（如灯泡的寿命、学生的 身高等)时，要考虑与这一数量指标相联系的随机试验， 对这一数量指标（随机变量）进行试验或观察。 总体：试验的全部可能的观察值. 有可能重复，} 个体：每一个可能观察值 不一定有限 1 总体是所研究的对象的某个（或某些）数量指标的全体，它 是一个随机变量（或多维随机变量），记为X. 以后不区分总体与相应的随机变量，统称为总体X 的分布函数和数字特征称为总体的分布函数和数字特征 总体的容量；有限总体；无限总体

研究有关对象的某一数量指标（如灯泡的寿命、学生的 身高等）时，要考虑与这一数量指标相联系的随机试验， 对这一数量指标（随机变量）进行试验或观察。 总体：试验的全部可能的观察值 . 总体是所研究的对象的某个(或某些)数量指标的全体,它 是一个随机变量(或多维随机变量)，记为X . 以后不区分总体与相应的随机变量，统称为总体X . 一、总体与个体 个体：每一个可能观察值. X的分布函数和数字特征称为总体的分布函数和数字特征. 总体的容量；有限总体；无限总体。 有可能重复， 不一定有限

实例：在研究2000名学生的身高时，这些学生的身高的全体就 构成一个总体，每个学生的身高就是个体. 总体服从某一分布：总体中的观察值是这一分布的随机变量的值 例如，检验自生产线出来的零件是正品(1)还是次品(0).设出现 正品的概率为p 这个总体是由一些0、1组成的，它对应于一个0-1分布的 随机变量X,其分布律为： X01 pfx=x)-p'a-p)(x=0.1)p 1-p p “总体服从(0-1)分布”是指总体中的观察值是(0-1)分布 的随机变量X的值

实例： 在研究2000名学生的身高时, 这些学生的身高的全体就 构成一个总体，每个学生的身高就是个体 . (1) (0). p. 例如 检验自生产线出来的零件是正品 还是次品 设出现 正品的概率为 ，   ( ) 1 (1 ) 0,1 x x P X x p p x − = = − = 是指总体中的观察值是(0-1)分布 这个总体是由一些0 1 0 -1 、组成的，它对应于一个 分布的 “总体服从(0-1)分布” 随机变量X, 其分布律为： 的随机变量X的值. 0 1 1 X P p p − 或 总体服从某一分布：总体中的观察值是这一分布的随机变量的值

二、简单随机样本 在实际中，总体的分布一般是未知的，或只知道它具有某 种形式，其中包含着未知参数。 为推断总体分布或其各种特征，按一定规则从总体中抽 取若干个体进行观察试验，以获得有关总体的信息，这一抽 取过程称为“抽样” 所抽取的部分个体称为总体的一个样本。 样本中所包含的个体数目称为样本容量

二、简单随机样本 为推断总体分布或其各种特征，按一定规则从总体中抽 取若干个体进行观察试验，以获得有关总体的信息，这一抽 取过程称为“抽样”. 在实际中，总体的分布一般是未知的，或只知道它具有某 种形式，其中包含着未知参数。 所抽取的部分个体称为总体的一个样本。 样本中所包含的个体数目称为样本容量

从总体抽取一个个体，就是对总体X进行一次观察， 并记录其结果. 在相同的条件下对总体X进行次重复的、独立的观察， 观察结果按试验次序记为X1,X2,.,Xm 第i次抽取的结果用X,(i=1,2,.)表示. 由于各次观察是在相同条件下独立进行的，可以认为 X1,X2,X,相互独立且与总体X同分布，这样得到的X1,X2, .,X,称为来自总体的一个简单随机样本，为样本容量. 当次观察一经完成，就得到一组实数x1,x2,.,xn它们依次 是随机变量X,X2,.,X,的观察值，称为样本值

1 2 , , , n X n X X X 在相同的条件下对总体 进行 次重复的、独立的观察， 观察结果按试验次序记为 . 1 2 1 2 , , , . , , , n n X X X n X X X X 相互独立且与总体 同 由于各次观察是在相同条件下独立进行的，可以认为 这样得到的 称 分布， 为来自总体的一个简单随机样本， 为样本容量 1 2 1 2 , . , , , , , n n n x x x X X X 当 次观察一经完成，就得到一组实数 它们依次 是随机变量 的观察值，称为样本值 从总体抽取一 就是对总体X进行一次观察， 并记录 个个体， 其结果. ( 1,2, ) . i 第i X i 次抽取的结果用 = 表示

说明： (1)对于有限总体，当总体容量N比要得到的样本容量n 大得多时，常将不放回抽样近似地当做放回抽样来处理，即 把不放回抽样得到的样本近似地看作简单随机样本。 代替的条件是Y≥10（其中N为总体容量，n为样本容量） (2)对于无限总体，采用不放回抽样，得到的样本总看作 是简单随机样本

（1）对于有限总体，当总体容量N比要得到的样本容量n 大得多时，常将不放回抽样近似地当做放回抽样来处理，即 把不放回抽样得到的样本近似地看作简单随机样本。 （2）对于无限总体，采用不放回抽样，得到的样本总看作 是简单随机样本。 说明： 10( ) N N n n 代替的条件是  其中 为总体容量， 为样本容量