山东理工大学：《线性代数》课程教学课件（PPT讲稿）第三章 矩阵的运算 3-1 矩阵的运算

©少本理工大写 课前复习 矩阵的初等变换(Elementary transformation) (ec); 初等行（列）变换{ ×k(c:×); +kr;(c:+kc) 2、子式与阶子式 3、秩的定义及性质 in Aun,f（1)3D,≠0；（2)VD+1=0. 则称为矩阵的最高阶非零子式.最高阶非零子式 的阶数称为矩阵的秩，记为r(或 R(A 返回

２、子式与 阶子式 k ３、秩的定义及性质 １、矩阵的初等变换（Elementary transformation） 初等行(列)变换 ( ) ; i j i j r r c c   ( ) ; i i r k c k   ( ) . i j i j  r kr c kc + +       , m n in A if  0 ;   D r 1 0 . （1） （2）  = D r+ 则 称为矩阵 的最高阶非零子式. D r A 记为 r(A或) R. (A) 最高阶非零子式 的阶数称为矩阵的秩， 课前复习

4、如果矩阵A经过有限次初等变换变成矩阵B 就称矩阵A与B等价，记作A~B 5、矩阵等价具有的性质 反身性； 对称性； 传递性， 6、利用初等行变换可把矩阵化为行阶梯形矩阵 利用初等行变换，也可把矩阵化为行最简形矩阵 利用初等行变换，再利用初等列变换最后可把矩阵 化为标准形矩阵. 最高阶非零子式的阶数 7、 矩阵的秩 =行阶梯形矩阵非零行的行数 行最简形矩阵非零行的行数 标准形矩阵中单位矩阵的阶数

４、如果矩阵 A 经过有限次初等变换变成矩阵 B ， 就称矩阵 A B 与 等价 ，记作 A B~ ５、矩阵等价具有的性质 反身性; 对称性; 传递性. 利用初等行变换可把矩阵 A 化为行阶梯形矩阵. 利用初等行变换，也可把矩阵化为行最简形矩阵. ６、 利用初等行变换，再利用初等列变换最后可把矩阵 化为标准形矩阵. ７、矩阵的秩 = 最高阶非零子式的阶数 = 行阶梯形矩阵非零行的行数 = 行最简形矩阵非零行的行数 = 标准形矩阵中单位矩阵的阶数 

©少本理上大罗 第三章矩阵的运算 ·第一节矩阵的运算 ·第二节逆矩阵 ·第三节初等矩阵 第四节分块矩阵 上 区回

第三章 矩阵的运算 • 第一节 矩阵的运算 • 第二节 逆矩阵 • 第三节 初等矩阵 • 第四节 分块矩阵

©山东理工大军 第一草矩阵的运算 六 五四三二 七共就麵阵 延降的幂 乘数如 方降的行到式 疑阵的转置 法乘

©少东理工大军 一、矩阵的加法 1、定义 设有两个m×n矩阵A=(a,)B-(b,)那末矩阵 A与B的和记作A+B,规定为 01+b1 a2+b2 1m+b a21+b2 a2+b2 A+B= am+bm am2+m2 am+b 说明只有当两个矩阵是同型矩阵时，才能进 行加法运算

１、定义               + + + + + + + + + + = m m m m m n m n n n n n a b a b a b a b a b a b a b a b a b A B        1 1 2 2 21 21 22 22 2 2 11 11 12 12 1 1 一、矩阵的加法 设有两个 矩阵 那末矩阵 与 的和记作 ，规定为 mn A (a ), B (b ), = ij = ij A B A+ B 说明 只有当两个矩阵是同型矩阵时，才能进 行加法运算

©中东X王大军 2、 矩阵加法的运算规律 ()A+B=B+A; (2)(A+B)+C=A+(B+C) -l12 一1n (3)-A= -0l22 =(-aj} 称为矩阵A的负矩阵 (④)A+（-A)=0,A-B=A+(-B) 上页

2、 矩阵加法的运算规律 (1) A+ B = B + A; (2)(A+ B)+ C = A+ (B + C). ( )               − − − − − − − − − − = m m m n n n a a a a a a a a a A        1 1 21 22 2 11 12 1 3 (4) A+ (− A) = 0, A− B = A+ (− B). ( ), = − aij 称为矩阵A的负矩阵

©少东理上大军 二、数与矩阵相乘 1、定义 数2与矩阵4的乘积记作乳A或A2,规定为 211 2L12 21n 2A=A2= 221 222 22n . Aam Aam Amn 区回

1、定义 . 1 1 2 1 2 2 2 1 1 1 2 1               = = m m mn n n a a a a a a a a a A A                   二、数与矩阵相乘 数与矩阵A的乘积记作A或A,规定为

©中东罪工大至 运算规律 （设AB的是 柜阵， 2,μ∈R (1)1A=A (2)2(4A)=(24)A (3)(A+B)=A+2B (4)(2+四)A=元A+uA (5)0A=0 (6)20=0 注意：1)数乘矩阵是数去乘A中的每一个元素 2)若2A=,0测 2=0.0r.A=0 .0r.2=0.nd.A=O 矩阵的加法与数乘矩阵合称为矩阵的线性运算， 上页

2、运算规律 （设 A B C 均是 m n 矩阵，  ）  ,  R （1） 1A A = （2）    ( ) ( ) A A = （3）    ( ) A B A B + = + （4） ( )     + = + A A A （6） O O= 注意: 1）数乘矩阵是数λ去乘Ａ中的每一个元素. （5） 0A O= 2）若 A O= ，则   = = = = 0 . . . . 0. . or A O or and A O 矩阵的加法与数乘矩阵合称为矩阵的线性运算

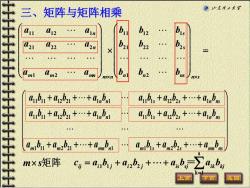
三、 矩阵与矩阵相乘 ©少东理工大罩 12 [n b12 L21 22 b22 m Am2 b b aubu+apx+anb aubis +absa aub+ax+anb a1b,+02b2,+.+a1bnw 0nibi+am,bi+.+anbnL0nib,+0mb,t+anmbe m×s矩阵c=aib,+a2b,+.+ab,-∑ab 上页 区回

m m mn m n n n a a a a a a a a a                       1 2 2 1 2 2 2 1 1 1 2 1 =                n n ns ns s s b b b b b b b b b        1 2 2 1 2 2 2 1 1 1 2 1 11 11 12 21 1 1 11 1 12 2 1 11 11 12 21 1 1 11 1 12 2 1 1 11 2 21 1 1 1 2 2 n n s s n ns n n s s n ns m m mn n m s m s mn ns a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b   + + + + + +   + + + + + +       + + + + + +   m s矩阵 三、矩阵与矩阵相乘 = = + + + 1 1 2 2  1 ij i j i j is sj ik kj c a b a b a b a b ｓ ｋ ＝

©)少东X子大军 1、 定义若A=(a,)mxsB=(b)xn, 规定AB=C=(C)mxn, 其中cy=a,+a,b++ab,∑4bg k （i=1,2,.,m;j=1,2,.,D 注：1)条件左矩阵A的列数等于右矩阵B的行数 2)方法左行右列法—矩阵乘积的元素 等于左矩阵的第行与右矩阵的第列对应元素 乘积的和. 3)结果左行右列一左矩阵A的行数为乘积 C的行数，右矩阵B的列数为乘积C的列数， 王

1、定义 ( ) , AB C c = = ij m n ( ) ( ) , 若 A a B b = = ij m n   s s ， ij 规定 1 1 2 2 1 ij i j i j is sj ik kj c a b a b a b a b = = + + +  ｓ ｋ 其中 ＝ （i m j n = = 1 2 1 2 ， ，； ， ，） 注： 1）条件 左矩阵Ａ的列数等于右矩阵Ｂ的行数 2）方法 C ij c 等于左矩阵 的第 行与右矩阵 的第 列对应元素 左行右列法——矩阵乘积 的元素 A i B j 乘积的和. 3）结果 左行右列——左矩阵Ａ的行数为乘积 Ｃ的行数，右矩阵Ｂ的列数为乘积Ｃ的列数