《概率论与数理统计》课程教学资源（PPT课件）8.3 正态总体方差的假设检验

第三节正态总体方差的假设检验 一、单个总体的情况 二、两个总体的情况

一、单个总体的情况 第三节 正态总体方差的假设检验 二、两个总体的情况

一、单个总体的情况 1.未知山，检验o 设总体X~N(4,o2),4,σ均未知，X,.,X,为来自 总体X的一个样本，显著性水平为. 检验假设：H:o2=o2,H1:o2≠o 原父-心e时，- 因ES)=0,当H,为真时，观察值S与σ的比 2,一般 应在1附近摆动，而不应过分大于1或过分小于1 拒绝域的形式为 n-1)S2 D2≤k,或，n二)。>之k

一、单个总体的情况 设总体 2 2 X N~ ( , ), ,     均未知， 1 , , X Xn， 为来自 总体 X 的一个样本，显著性水平为 . 2 1.未知  ，检验 检验假设: 2 2 2 2 0 0 1 0 : , : H H     =  2 2 2 0 2 S H S   当 为真时，观察值 与 的比 ， 一般 应在1 1 1 附近摆动，而不应过分大于 或过分小于 2 2 因E S( ) =  ， 2 2 2 ( 1) , n S   − 取 = 2 0 2 ( 1) n S H  − 真时， 2 ~ ( 1),  n− 拒绝域的形式为 2 2 2 2 1 2 0 0 ( 1) ( 1) n S n S k k   − −   或

拒绝域的形式为 (n-)S2 k或n-)≥ k2 P{H为真时拒绝H,} -小 k=光en-k=x2n-, 拒绝域为 a心s-w&a5m-

0 2 2 2 2 1 2 0 0 ( 1) ( 1) H n S n S P k k           − − =                 = , 拒绝域的形式为 2 2 2 2 1 2 0 0 ( 1) ( 1) n S n S k k   − −   或 P H H  0 0 为真时拒绝  2 2 2 1 0 2 ( 1) ( 1) n S   n  − −  − 2 2 2 0 2 ( 1) ( 1) n S   n  −  − 2 1 1 2 k n( 1),   −  = − 2 2 2 k n( 1), = −   拒绝域为 或

单边检验问题 设总体X~N(4,o2),4,o2均未知，X1,Xn,为来自 总体X的一个样本，显著性水平为. 检验假设H:o2≤o,H1:o2>o 二右边检验 因H中的全部σ都比H中的o2要小，当H为真时， S2的观察值往往偏大（概垮域的形式为S2≥k. 下面确定常数k,P档H为真时拒绝H}=Pa{S2≥k, "5a 上式中取等 k'(n-1)s (n-D)s o? ≥x2-

2 2 0 2 P S k { },   =  2 2 0 2 2 0 ( 1) n S P k       − =      2 2 0 2 2 ( 1) n S P k        −        , 单边检验问题 设总体 2 2 X N~ ( , ), ,     均未知， 1 , , X Xn， 为来自 总体 X 的一个样本，显著性水平为. 检验假设 2 2 2 2 0 0 1 0 H H : , :       2 2 因H H 0 1 中的全部  都比 中的 要小， 2 因此，拒绝域的形式为 S k  . 下面确定常数k ， 0 0 P H H { } 当 为真时拒绝 2 S 的观察值往往偏大. 上式中取等号知 2 k n( 1)    = − 2 2 2 0 ( 1) ( 1) n S   n  −   − —— 右边检验 当H1为真时， 2 2 0 ( 1) n S  −• 2 2 ( 1) n S  −• k   (小概率事件)

右边检验问题：H:σ2≤σ，H1:σ2>o 拒绝域为 u-S'≥n- ■ 一一一一一一一一一一 同理，左边检验问题：H。:σ2≥o,H1o2<σ 拒绝域为 -0ss.n-0

右边检验问题： 2 2 2 2 0 0 1 0 H H : , :       拒绝域为 2 2 2 0 ( 1) ( 1) n S   n  −  − 同理，左边检验问题： 2 2 2 2 0 0 1 0 H H : , :       拒绝域为 2 2 2 1 0 ( 1) ( 1) n S   n  − −  −

例某厂生产的某种型号的电池，其寿命长期以来服从方差 σ2=5000（小时2）的正态分布，现有一批这种电池，从它生产情况 来看，寿命的波动性有所变化。现随机的取26只电池，测出其寿 命的样本方差s2=9200(小时)。问根据这一数据能否推断这批电 池的寿命的波动性较以往的有显著的变化？(a=0.02) x-N(u,o' 解：检验假设H:o2=5000=o,H1:σ2≠5000 拒绝域为 0-ssxm-0=11-524 2 或 u-lS≥x,0n-l=4,314 计算：n=26,=5000=→m-)S'-25×920-46>44.314 02 5000 所以拒绝H,认为这批电池的寿命的波动性较以往的有 显著的变化

例 某厂生产的某种型号的电池，其寿命长期以来服从方差 σ 2 = 5000 (小时2 )的正态分布，现有一批这种电池，从它生产情况 来看，寿命的波动性有所变化。现随机的取26只电池，测出其寿 命的样本方差s 2 = 9200(小时2 )。问根据这一数据能否推断这批电 池的寿命的波动性较以往的有显著的变化? ( ) 2 X N , ( 0.02)  = 解： 检验假设 2 2 2 0 0 1 : 5000 , : 5000 H H    = =  2 2 2 1- /2 0 ( 1) ( -1) n S   n  −  = 11.524 2 2 2 / 2 0 ( 1) ( -1) n S   n  −  = 44.314 拒绝域为 或 2 2 0 ( 1) n S  − 25 9200 5000  = = 46  44.314 2 0 n = = 26 5000 ，  所以拒绝H0，认为这批电池的寿命的波动性较以往的有 显著的变化。 计算:

补例某种导线要求电阻的标准差不得超过0.0052，今在生产 的一批导线中取样品9根，测得S=0.0072。设总体服从正态分 布，在显著性水平a=0.05条件下，能认为这批导线的标准差显 著偏大吗？ X~N(山，σ2）)样本信息偏大，用右边检验 解：检验假设H。:o≤o,=0.005;H1:o>0.005, 拒绝域为X_1-S o ≥x2(n-1)=15.507 计算得X2=9-)x0.007 =15.68>15.507, 0.052 所以拒绝原假设，认为标准差显著偏大

补例 某种导线要求电阻的标准差不得超过 0.005Ω，今在生产 的一批导线中取样品 9 根，测得 S=0.007Ω。设总体服从正态分 布，在显著性水平 α = 0.05 条件下，能认为这批导线的标准差显 著偏大吗? 2 2 2 0 ( 1) n S   − = = 15.507  15.507, 2  −  ( 1) n 解: 0 0 1 检验假设 H H : 0.005; : 0.005     =  ， 拒绝域为 计算得 = 15.68 所以拒绝原假设，认为标准差显著偏大. ( ) 2 X N , 样本信息偏大，用右边检验 2 2 2 (9 1) 0.007 0.05  −  =

内容小结 一、单个总体的情况 1.未知山，检验σ 双检验问题：H:o2=o2,H1:o2≠o, 拒绝域为 “a-速 (n-1)S2 02 ≥Xa(n-1) 2 右边检验问题：Ho2≤o,H1:o2>o 拒绝域为 n-s'≥x2n-0 左边检验问题： H:o2≥o,H1:o2<o 拒绝域为 n-ns'sxn-l）

一、单个总体的情况 2 1.未知  ，检验 双检验问题: 2 2 2 2 0 0 1 0 : , : H H     =  2 2 2 1 0 2 ( 1) ( 1) n S   n  − −  − 2 2 2 0 2 ( 1) ( 1) n S   n  − 拒绝域为 或  − 右边检验问题： 2 2 2 2 0 0 1 0 H H : , :       拒绝域为 2 2 2 0 ( 1) ( 1) n S   n  −  − 左边检验问题： 2 2 2 2 0 0 1 0 H H : , :       拒绝域为 2 2 2 1 0 ( 1) ( 1) n S   n  − −  − 内容小结

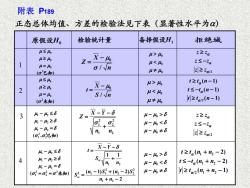
附表P189 正态总体均值、方差的检验法见下表（显著性水平为） 原假设H。 检验统计量 备择假设H 拒绝域 4≤A z=X-4 μ>% zZZa 4≥4 1 μ=h μ4% i2ta(n-1) 2 4≥% t≤-te(n-1) μ=4， S/√n 46 z2La 4-4≥6 L-h6 t≥ta(n1+n2-2) 4 t≤-ta(n+n2-2) 4-4=6 +可 4-h<6 (o1=o=σ2未知) S=4-0S+%-2S L-4≠8 l4≥ta2(n1+n2-1) %1+n2-2

4 1 2 1 2 1 2 222 1 2 ( )           −  −  − = = = 未知 0 0 0          −  −  −  1 2 1 2 /2 1 2 ( 2) ( 2) ( 1) t t n n t t n n t t n n     + −  − + −  + − 1 2 2 2 2 1 1 2 2 1 2 1 1 ( 1) ( 2) 2 w w X Y t S n n n S n S S n n − −  = + − + − = + − 原假设H0 检验统计量 备择假设H1 拒绝域 0 0 0 2 ( )          = 已知 0 0 0 2 ( )          = 未知 1 2 1 2 1 2 2 2 1 2 ( , )            −  −  − = 已知 0 / X Z n   − = 0 / X t S n −  = 2 2 1 2 1 2 X Y Z n n    − − = + 0 0 0          0 0 0          0 0 0          −  −  −  /2 z z z z z z      −  /2 ( 1) ( 1) ( 1) t t n t t n t t n     −  − −  −/2 z z z z z z      −  3 2 1 附表 P189 正态总体均值、方差的检验法见下表（显著性水平为）

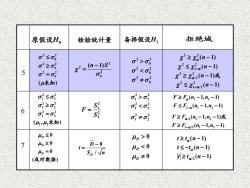
原假设H。 检验统计量 备择假设H 拒绝域 a2≤o G220p g2>gi x2≥x2(n-1) x2≤.n-) 5 x2=n-10s2 a2=0u a g2o2 F2F.h-1,2-1) Gi203 oi0 t≥ta(n-1) 7 4≥0 D-0 4o=0 S/√n 4D<0 t≤-t.(n-l) (成对数据) 4o≠0 t≥ta2(n-1)

7 2 2 1 2 2 2 1 2 2 2 1 2 1 2 ( , )         =未 知000 ( ) DDD = 成对数据 0 / DD t S n − = 000 DDD   / 2 ( 1) ( 1) ( 1) t t n t t n t t n    −  − −  − 2 20 2 20 2 20 ( )       =未知 2 2 20 ( 1) n S  − = 2122 S F S = 2 20 2 20 2 20        2 2 2 21 2 2 / 2 2 2 1 /2 ( 1) ( 1) ( 1) ( 1) nnn n             −−  −  −  −  − 或 65 原 假 设H0 检 验 统 计 量 备 择假 设H1 拒 绝 域 2 2 1 2 2 2 1 2      1 2 1 1 2 ( 1, 1) ( 1, 1) F F n n F F n n  −  − −  − − /2 1 2 或 1 /2 1 2 ( 1, 1) ( 1, 1) F F n n F F n n  −  − −  − − 2 2   1 2 