山东理工大学：《线性代数》课程教学课件（PPT讲稿）第二章 矩阵与向量 2-2 向量及其线性运算

©山东理工大军 第二节向量及其线性运算 上页

第二节 向量及其线性运算

⑤少本开上大军 一、n维向量（Vector). 、定义2.2.1n个实数组成的有序数组称为n维向量.一 般用a,阝，等希腊字母表示. 2、0=(1,02, ,0n） n维行向量 4;称为向量a的第i 个分量 B= n维列向量 它们的区别 只是写法上 的不同。 上页 回

( , , , )  = a1 a2  an n维行向量 1 2 b b bn        =         n维列向量 ai称为向量的第i 个分量 n个实数组成的有序数组称为n维向量.一 般用 ,  , 等希腊字母表示. 1、定义2.2.1 它们的区别 只是写法上 的不同。 一、ｎ维向量（Vector） 2

©本理工大军 3、分量全为零的向量(0,0，.，0) 称为零向量。 4、 向量相等：如果n维向量 a=(a,4,an）f=(b,b,.,bn) 的对应分量都相等，即4，=b,(i=1,2,n) 就称这两个向量相等，记为Q=B 5.负向量：-a=(41-4,.-0）

3、分量全为零的向量 (0,0, ,0) 称为零向量。 4、向量相等：如果n 维向量 ( ) 1 2 , , , n  = a a a ( ) 1 2 , , , n  = b b b 的对应分量都相等，即 1,2, , ( ) i i a b i n = = 就称这两个向量相等，记为   = 5、负向量： ( ) n − = − a − a  − a  1 2

向量的运算 1、 加法a=(aa2.an),B=(bb,.b), 规定a+B=(a1+b,a2+b2.an+bn) 称为α与的和向量， a-B=a+(-B)=(a-bi a2-b2.an-b) 称为a与的差向量 2、数乘a=（a12.an),k∈R 规定ka=ak=（k1ka2·kan) 称为数k与向量a的数量积. 向量的加法与数乘合称为向量的线性运算. 区回

    − = + − = − − − ( ) (a b a b a b 1 1 2 2 n n ) k k ka ka ka  = = ( 1 2 n ) 二、向量的运算   + = + + + (a b a b a b 1 1 2 2 n n ) 1、加法   = = (a a a b b b 1 2 1 2 n n ), , ( ) 规定 2、数乘 ( 1 2 ), n  =  a a a k R 规定 称为数ｋ与向量α的数量积. 向量的加法与数乘合称为向量的线性运算. 称为α与β的和向量. 称为α与β的差向量

©少东理工大军 4、 运算律： (1)a+B=B+a (5)1·a=a (2)(a+B)+y=(a+B)+Y(6)k(la)=(k)a (3)a+0=a (7)(k+Da=ka+la (4)a+(-a)=0 (8)k(a+B)=ka+kB 注：(1) 对任意的向量Q,存在唯一的零向量0， 使得a+0=0 (2)对任意的向量a,存在唯一的负向量-0， 使得a+（(-a)=0 (3)0a=0;(-1)a=-a;20=0. (4)如果0=0，则入=0或a=0 上页

(4) ( ) 0 (3) 0 (2)( ) ( ) (1) + − = + = + + = + + + = +               ( ) (  )          k k k k l k l k l kl + = + + = + =  = (8) (7) (6) ( ) ( ) (5)1 4、运算律： 注：（1）对任意的向量 , 存在唯一的零向量 o, 使得   + = o （2）对任意的向量 , 存在唯一的负向量 −, 使得   + − = ( ) o （4）如果 = 0, 则  = = 0 0 或 （3） 0 0; ( 1) ; 0 0.     = − = − =

⑤少东X大军 三、应用举例 例1c,=(110)',a2=(011)'a,=(340) a=3a+2a,-a3 B=a-a,+a3 解 a+-ai+214 0 =(012). =01 =(44 -.( 回

解 (4 4 1 . ) T = − 1 0 3 3 1 2 1 1 4 0 1 0             = + −                   (0 1 2 . ) T =     = − + 1 2 3 0 1 2     =       1 0 3 1 1 1 1 1 4 0 1 0             = − +                   4 4 1     =       −     = − + 1 2 3 1 2 3     = + − 3 2 例1 ( ) 1 1 1 0 T  = ， ( ) 3 340 T 2 (0 1 1)  = T  = ， 求 1 2 3     = + − 3 2 三、应用举例

©山东理工大军 四、 向量空间 1、 定义设V为n维非空向量组，且满足 ①对加法封闭 fa∈V,B∈V→a+B∈V; ②对数乘封闭 fa∈V,2∈R→λa∈V. 那么就称向量组V为向量空间(Vector Space) 例1、全体n维向量所组成的集合是一个向量空间 记作： R={x1x2.xn)引x,x2,xn∈R}

例1、全体ｎ维向量所组成的集合是一个向量空间, R (x x xn ) x x xn R n = 1 2  | 1 , 2 ,  ,  if V V V        +  , ; 四、向量空间 1、定义 设Ｖ为ｎ维非空向量组，且满足 ①对加法封闭 ②对数乘封闭 那么就称向量组Ｖ为向量空间（Vector Space）． if V R V        , . 记作 ：

王 》东大 例2判别下列集合是否为向量空间. Dy={=(0.x)s,xeR 解fa=(0a.a)Jey,B=(0b.b)'e 有 a+B=(0a2+b,.an+bn)'∈， keR,有ka=(0ka,.km)'ey, 所以V是一个向量空间. 2)={=l.x小sx∈风 解fa=(1a.an）'∈ 3k=2,使2a=（2202.2an)V2, 所以V,不是一个向量空间： 回

例2 判别下列集合是否为向量空间. 1 2 2  (0 , , )  T V x x x x x R = =  n n 1 ) 2 2 2  (1 , , )  T V x x x x x R = =  n n 2 ) 解 (0 , 0 2 1 2 1 ) ( ) T T n n if a a V b b V   =  =  (0 , 2 2 1 ) T n n 有   + = + +  a b a b V , 0 , ( 2 1 ) T n   =  k R k ka ka V 有  所以 是一个向量空间. V1 解 (1 2 2 ) T n if a a V  =  2, 2 2 2 2 , ( 2 2 ) T n  = =  k a a V 使  所以 不是一个向量空间. V2

例3设a,B为两个已知的n维向量试判断集合 V={x=a+邺，μeR是否为向量空间. 解fx1=+山B,x2=20+凸B 有x,+x2=(2+2)a+(41+h2)B∈V Vk∈R,3c1=k2a+khB∈V 所以”是一个向量空间 2、子空间 定义：设有向量空间及，若有∈.则称M 是的子空间. 实例：设是由维向量所组成的向量空间，显然 VR”,所以总是R的子空间

V x R = = +      ,  例3 设α,β 为两个已知的ｎ维向量试判断集合 是否为向量空间. 解 1 1 1 2 2 2 if x x = + = +         , 有 x x V 1 2 1 2 1 2 + = + + +  (      ) ( ) 1 1 1    = +  k R kx k k V ,     所以 V 是一个向量空间. 2、子空间 定义:设有向量空间V1及V2 , 若有V1V2 . 则称V1 是V2的子空间. 实例: 设V是由n维向量所组成的向量空间, 显然 VRn , 所以V总是Rn的子空间

⑨少本理上大罩 小结 向 解析几何 (n≤3) 线性代数 坐 ↓ 既有大小又有方向的量 有次序的实数组成的数组 标 几何形象：可随意 代数形象：向量的 平行移动的有向线段 坐标表示式 =(4a2.an) 回

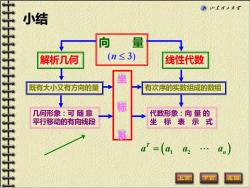
向 量 解析几何 (n  3) 线性代数 既有大小又有方向的量 有次序的实数组成的数组 几何形象：可 随 意 平行移动的有向线段 代数形象：向 量 的 坐 标 表 示 式 ( 1 2 ) T n a a a a = 坐 标 系 小结