《高等数学》课程教学资源（PPT课件）第八章 向量代数与空间解析几何_8-3 平面及其方程

第三节 第八章 平面及其方程 平面的点法式方程 二、平面的一般方程 三、两平面的夹角

一、平面的点法式方程 二、平面的一般方程 三、两平面的夹角 平面及其方程 第八章

曲面方程的概念 引例：求到两定点4A(1,2,3)和B(2,-1,4)等距离的点的 轨迹方程. 解：设轨迹上的动点为M(x,y,z),则AM=BM,即 V(x-1)2+(y-2)2+(z-3)2 =V(x-2)2+(y+1)2+(z-4) 化简得2x-6y+2z-7=0 说明：动点轨迹为线段AB的垂直平分面. 显然在此平面上的点的坐标都满足此方程， 不在此平面上的点的坐标不满足此方程

求到两定点A(1,2,3) 和B(2,-1,4)等距离的点的 2 2 2 (x 1)  ( y  2)  (z  3) 化简得 2x  6y  2z  7  0 即 说明: 动点轨迹为线段 AB 的垂直平分面. 引例: 显然在此平面上的点的坐标都满足此方程, 不在此平面上的点的坐标不满足此方程. 2 2 2  (x  2)  ( y 1)  (z  4) 解:设轨迹上的动点为M (x, y,z),则 AM  BM , 轨迹方程

定义 如果曲面S与方程F(x,yz)=0有下述关系 (1)曲面S上的任意点的坐标都满足此方程， (2)不在曲面S上的点的坐标不满足此方程」 则F(x,yz)=0叫做曲面S的方程 F(x,y,2)=0 曲面S叫做方程F(x,yz)=0的图形 两个基本问题： 1)） 已知一曲面作为点的几何轨迹时 求曲面方程 (2)已知方程时，研究它所表示的几何形状 (必要时需作图)

定义 F(x, y,z)  0 S z y x o 如果曲面 S 与方程 F( x, y, z ) = 0 有下述关系: (1) 曲面 S 上的任意点的坐标都满足此方程; 则 F( x, y, z ) = 0 叫做曲面 S 的方程, 曲面 S 叫做方程 F( x, y, z ) = 0 的图形. 两个基本问题 : (1) 已知一曲面作为点的几何轨迹时, (2) 不在曲面 S 上的点的坐标不满足此方程, 求曲面方程. (2) 已知方程时 , 研究它所表示的几何形状 ( 必要时需作图 )

一、平面的点法式方程 设一平面通过已知点M(x0,yo,2o)且垂直于非零向 量=(A,B,C),求该平面Π的方程 任取点M(x,y,)∈卫，则有 MoM Ln 故 MoM.n=0 M0M=(x-0,y-0,2-20） 4(x-xo)+B(y-yo)+C(2-20)=0 称①式为平面Π的点法式方程，称为平面Ⅱ的法线向量

 z y x o M0 n ① 一、平面的点法式方程 ( , , ) 0 0 0 0 设一平面通过已知点 M x y z 且垂直于非零向 ( ) ( ) ( ) 0 A x  x0  B y  y0  C z  z0  M 称①式为平面的点法式方程, 求该平面的方程. 任取点M (x, y,z), ( , , ) 0 0 0 x  x y  y z  z 法线向量 量 n  (A , B, C), M M n 0 0 M0M n  M0M  则有 故 称 n 为平面 的

例1.求过三点M1(2,-1,4),M2(-1,3,-2),M3(0,2,3) 的平面Π的方程 解：取该平面江的法向量为 n=MM2×M1M3 M3 =-34-6 -23-1 =(14,9,-1) 又M,利用点法式得平面Π的方程 14(x>2)+9(y+1)-(2-4)=0 即 14x+9y-2-15=0

i j k  例1 , 又M1   (14, 9, 1) 14(x  2)  9( y 1)  (z  4)  0 即 14x  9y  z 15  0 M1 M2 M3 解: 取该平面 的法向量为 ( 2, 1,4), ( 1,3, 2), M1  M2   (0,2,3) M3 的平面  的方程. 利用点法式得平面  的方程   3 4  6  2 3 1 n n  M1M2  M1M3

说明：此平面的三点式方程也可写成 x-2y+1z-4 -3 4 -6=0 -2 3 般情况：过三点Mk(xk,yk,2k)(k=1,2,3) 的平面方程为 X-X y-y1 2-21 x2-1y2-y1 22-21 =0 X3二X1 Z3-Z1

此平面的三点式方程也可写成 0 2 3 1 3 4 6      x  2 y 1 z  4 0 3 1 3 1 3 1 2 1 2 1 2 1 1 1 1           x x y y z z x x y y z z x x y y z z 一般情况 : 过三点 M (x , y ,z ) (k 1,2,3) k k k k 的平面方程为 说明

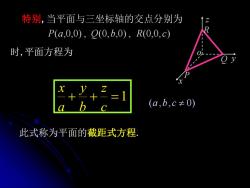
特别，当平面与三坐标轴的交点分别为 P(a,0,0),Q(0,b,0),R(0,0,c) 时，平面方程为 (a,b,c≠0) 此式称为平面的截距式方程

特别, 此式称为平面的截距式方程. P(a,0,0) , Q(0,b,0) , R(0,0,c)   1 c z b y a x 时, (a,b,c  0) 平面方程为 P o z y x R Q

二、平面的一般方程 设有三元一次方程 Ax+By+Cz+D=0(42+B2+C2+0) ② 任取一组满足上述方程的数x0,0,0,则 Ax0+By0+C20+D=0 以上两式相减，得平面的点法式方程 A(x-x0)+B(y-0)+C(2-0)=0 显然方程②与此点法式方程等价，因此方程②的图形是 法向量为n=(AB,C)的平面，此方程称为平面的一般 方程

二、平面的一般方程 以上两式相减 , 得平面的点法式方程 此方程称为平面的一般 Ax  By  Cz  D  0 任取一组满足上述方程的数 , , , 0 0 0 x y z 则 ( ) ( ) ( ) 0 A x  x0  B y  y0  C z  z0  0 A x0  B y0  C z0  D  显然方程②与此点法式方程等价, ( 0) 2 2 2 A  B  C  ② n(A,B,C) 的平面, 因此方程②的图形是 法向量为 方程

Ax+By+Cz+D=0(42+B2+C20) 特殊情形 ·当D=0时，Ax+By+Cz=0表示通过原点的平面； ·当A=0时，By+Cz+D=0的法向量 n=(0,B,C)⊥i,平面平行于x轴； ·A=B=0,Cz+D=0表示平行于xoy面的平面；

特殊情形 • 当 D = 0 时, A x + B y + C z = 0 表示通过原点的平面; • 当 A = 0 时, B y + C z + D = 0 的法向量 平面平行于 x 轴; • A = B = 0, C z + D = 0 表示 Ax  By  Cz  D  0 ( 0) 2 2 2 A  B  C  平行于 xoy 面 的平面; n  (0,B,C)  i

例2.求通过x轴和点(4，一3，-1)的平面方程 解：因平面通过x轴，故A=D=0 设所求平面方程为By+Cz=0 代入已知点(4，-3，-1)得C=-3B 化简，得所求平面方程y-3z=0 例3.用平面的一般式方程导出平面的截距式方程

例2. 求通过 x 轴和点( 4, – 3, – 1) 的平面方程. 例3.用平面的一般式方程导出平面的截距式方程. 解: 因平面通过 x 轴 , 故 A  D  0 设所求平面方程为 By  Cz  0 代入已知点(4,  3, 1)得 C  3B 化简,得所求平面方程 y  3z  0