《高等数学》课程教学资源（课件讲稿）第二章 导数与微分_2-1 导数概念

第之章 导数与微分 微积分学的创始人： 英国数学家Newton 德国数学家Leibniz 导数 描述函数变化快慢 微分学 微分 一描述函数变化程度

第二章 微积分学的创始人: 德国数学家 Leibniz 微分学 导数 描述函数变化快慢 微分 描述函数变化程度 导数与微分 英国数学家 Newton

第一节 导的橇念 一、引例 二、导数的定义 三、导数的几何意义 四、函数的可导性与连续性的关系 五、单侧导数

一、引例 二、导数的定义 三、导数的几何意义 四、函数的可导性与连续性的关系 五、单侧导数 第一节 导数的概念

一、引例 1.变速直线运动的速度 设描述质点运动位置的函数为 s口f(t) 则to到t的平均速度为 a f(t)口f(to】 自由落体运动 t口to s 03gt2 而在t,时刻的瞬时速度为 f(t)▣f(to) f(to) f(1 v▣lim o t to

一、 引例 1. 变速直线运动的速度 设描述质点运动位置的函数为 则 到 的平均速度为 而在 时刻的瞬时速度为 自由落体运动

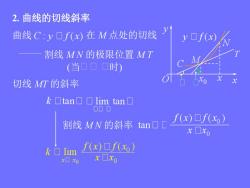
2.曲线的切线斜率 曲线C:y口f(x)在M点处的切线 yf(x)人 割线MN的极限位置MT (当口口口时)》 切线MT的斜率 k▣tan▣▣lim tan▣ 00▣ 割线MN的斜率tanOC f(x)口f(x) x□xo k▣lim f(x)口f(xo) xx0 x□xg

2. 曲线的切线斜率 曲线 在 M 点处的切线 割线 M N 的极限位置 M T (当 时) 割线 M N 的斜率 切线 MT 的斜率

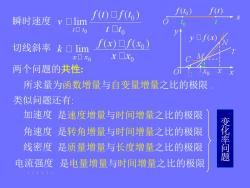
f(t)f(t) f(to) f(t) 瞬时速度 vlim t▣to t□to yf(x) 切线斜率k口lim f(x)口f(x)】 x口x0 x口xo 两个问题的共性： 所求量为函数增量与自变量增量之比的极限 类似问题还有： 加速度是速度增量与时间增量之比的极限 角速度是转角增量与时间增量之比的极限 线密度是质量增量与长度增量之比的极限 变化率问题 电流强度是电量增量与时间增量之比的极限

两个问题的共性: 瞬时速度 切线斜率 所求量为函数增量与自变量增量之比的极限 . 类似问题还有: 加速度 角速度 线密度 电流强度 是速度增量与时间增量之比的极限 是转角增量与时间增量之比的极限 是质量增量与长度增量之比的极限 是电量增量与时间增量之比的极限 变 化 率 问 题

二、导数的定义 定义1，设函数y口f(x)在点x,的某邻域内有定义， 若 limflim □y口f(x)☐f(x) x xo x口xo 0x00☐x 口x口x□xg 存在，则称函数∫(x)在点x处可导，并称此极限为 y口f(x)在点x的导数记作： yo；fo) dy df(x) dxx口xo dx x口xO 即 y,口fxo)口1im Cy 口xO0□x ▣lim f(x,回☐x)口f(xo】 lim f(xo☐h)▣f(x,》 0x00 口x h00 h

二、导数的定义 定义1 . 设函数 在点 存在, 并称此极限为 记作: 即 则称函数 若 的某邻域内有定义 , 在点 处可导, 在点 的导数

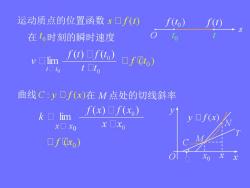
运动质点的位置函数s口f(t) f(to) f(t) 在o时刻的瞬时速度 to v☐lim f(t)口f(t) t□to ▣fqto) t加to 曲线C:y口f(x)在M点处的切线斜率 k▣1im f(x)口f(x) yf(x x▣x0 x口x0 ▣fxo)

运动质点的位置函数 在 时刻的瞬时速度 曲线 在 M 点处的切线斜率

若极限 lim f(x)☐f(x) 0lim 口y▣f(x)口f(x) x日x0 x口xO x00口X ▣x□x □xo 不存在，就说函数在点x不可导 若 也称f(x)在x的导数为无穷大 若函数在开区间/内每点都可导，就称函数在I内可导 此时导数值构成的新函数称为导函数 记作了)： dy.df(x) dx

不存在, 就说函数在点 不可导. 若 也称 在 若函数在开区间 I 内每点都可导, 此时导数值构成的新函数称为导函数. 记作: 就称函数在 I 内可导. 的导数为无穷大 . 若极限

则 注意了心)小水w

注意: 则

例1.求函数f(x)口C(C为常数)的导数 解：l口1imxO0)/四口1im C GC ▣0 0x00 □x ☐x▣0 □x 即 (C)更0 例2.求函数f(x)☐x”(n口N)在x口a处的导数 解：fa)口lim/)口f(a x"口a Olim x a x☐a x0ax□a O1im(xn0☐ax2☐a2xcuu☐ana） x▣a ☐nan☑

例1. 求函数 (C 为常数) 的导数. 解: 即 例2. 求函数 解: