《线性代数》课程教学课件（PPT讲稿，A）1.3行列式的计算

1.3n阶行列式的计算 Calculation of n-order determinant 4LL(LLL 山东理工大学数学系王玉田

1 . 3 n 阶 行列式的 计算 Calculation of n-order determinant 山东理工大学数学系 王玉田

◆n阶行列式的计算 本节将简单介绍利用行列式按行（列）展开的 定理和行列式的性质计算行列式的方法： 例1计算行列式 1 2-1 3/ 2 3 -1 2 D = -1 1 1 0 0 1 -2 1 n阶行列式的计算

n 阶行列式的计算 ◆ n阶行列式的计算 本节将简单介绍利用行列式按行（列）展开的 定理和行列式的性质计算行列式的方法. 例1 计算行列式 1 2 1 3 2 3 1 2 1 1 1 0 0 1 2 1 D − − = − −

◆n阶行列式的计算 解： 2 -1 3 1 2 -1 3 5-21 0 -1 1 -4 3+1 0 -1 1 -4 D -1 1 1 0 0 3 0 3 0 1 -2 1 0 1 -2 1 -1 1 -4 -1 1 -3 c3-C1 3 3 0 3 = 3 0 0 1 -2 1 1 -2 0 -3 -3 18 -2 0 n阶行列式的计算

n 阶行列式的计算 2 1 2 1 2 1 3 0 1 1 4 1 1 1 0 0 1 2 1 r r D − − − − = − − 3 1 1 2 1 3 0 1 1 4 0 3 0 3 0 1 2 1 r r + − − − = − 1 1 4 3 0 3 1 2 1 − − = − 3 1 1 1 3 3 0 0 1 2 0 c c − − − = − 1 3 3 18 2 0 − = − = − 解： ◆ n阶行列式的计算

◆n阶行列式的计算 例2计算行列式 a b c d a a+b a+b+c a+b+c+d D = a 2a+b _3a+26+c 4a+3b+2c+d a 3a+b 6a+3b+c 10a+6b+3c+d 解： a b c d r4-3 -2 0 L a+b a+b+c D 2- 0 a 2+b3a+2b+C 0 a 3a+b 6a+3b+c n阶行列式的计算

n 阶行列式的计算 例2 计算行列式 2 3 2 4 3 2 3 6 3 10 6 3 a b c d a a b a b c a b c d D a a b a b c a b c d a a b a b c a b c d + + + + + + = + + + + + + + + + + + + 4 3 3 2 2 1 0 0 2 3 2 0 3 6 3 r r r r r r a b c d a a b a b c D a a b a b c a a b a b c − − − + + + = + + + + + + 解： ◆ n阶行列式的计算

◆n阶行列式的计算 L a+b a+b+c =a L 2a+b 3a+2b+c a 3a+b 6a+3b+c a+b a+b+c a 2a+b 0 L 2a+b = a' a 3a+b 0 3a+b 注：以上两例都是首先通过性质5将行列式某一行（列 只保存一个非零元素，然后利用第二节定理1.2.1的推论， 降阶计算行列式的值，这是计算行列式常用的方法之一， n阶行列式的计算

n 阶行列式的计算 2 3 2 3 6 3 a a b a b c a a a b a b c a a b a b c + + + = + + + + + + 3 2 2 1 0 2 0 3 r r r r a a b a b c a a a b a a b − − + + + = + + 2 4 2 3 a a b a a a a b + = = + 注： 以上两例都是首先通过性质5将行列式某一行（列） 只保存一个非零元素，然后利用第二节定理1.2.1的推论， 降阶计算行列式的值，这是计算行列式常用的方法之一. ◆ n阶行列式的计算

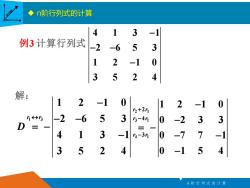
◆n阶行列式的计算 4 1 3 -1 例3计算行列式 -2 -6 5 3 1 2 -1 0 3 5 2 4 解： 1 2 -1 0 1 2 -1 0 2+2 1←今3 -2 -6 5 3 5-4r 0 -2 3 3 D 4 1 3 -1 4-31 0 -7 7 -1 3 5 2 4 0 -1 5 4 n阶行列式的计算

n 阶行列式的计算 例3 计算行列式 4 1 3 1 2 6 5 3 1 2 1 0 3 5 2 4 − − − − 1 3 1 2 1 0 2 6 5 3 4 1 3 1 3 5 2 4 r r D  − − − = − − 2 1 3 1 4 1 2 4 3 1 2 1 0 0 2 3 3 0 7 7 1 0 1 5 4 r r r r r r + − − − − = − − − − 解： ◆ n阶行列式的计算

◆n阶行列式的计算 1 2 -1 0 12 -1 0 2分4 0 -1 5 4 5-72 0 -1 5 4 三 0 -7 7 -1 4-22 0 0 -28 -29 0 -2 3 3 0 0 -7 -5 1 2 -1 0 1 2 -1 0 3r4 0 -1 5 4 4-453 0 -1 5 4 0 0 -7 -5 0 0 -7 -5 0 0 -28 -29 0 0 0 -9 =-1×(-1)×(-7)×(-9)=63 n阶行列式的计算

n 阶行列式的计算 2 4 1 2 1 0 0 1 5 4 0 7 7 1 0 2 3 3 r r  − − = − − − 3 2 4 2 7 2 1 2 1 0 0 1 5 4 0 0 28 29 0 0 7 5 r r r r − − − − = − − − − 3 4 1 2 1 0 0 1 5 4 0 0 7 5 0 0 28 29 r r  − − = − − − − − 4 3 4 1 2 1 0 0 1 5 4 0 0 7 5 0 0 0 9 r r − − − = − − − − = −  −  −  − = 1 ( 1) ( 7) ( 9) 63 ◆ n阶行列式的计算

◆n阶行列式的计算 1 例4设多项式 1 2 3 1 2-x2 2 3 f(x)= 2 3 1 5 2 3 1 9-x2 试求fx)的根. 解（方法一） 1 0 0 0 c2-C1 c3-2c1 1 1-x2 0 0 f(x) 三 4-3C1 2 1 -3 -1 2 1 -3 3-x2 n阶行列式的计算

n 阶行列式的计算 2 2 1 1 2 3 1 2 2 3 ( ) 2 3 1 5 2 3 1 9 x f x x − = − 例4 设多项式 试求f(x)的根. 解 (方法一) 2 1 3 1 4 1 2 2 3 2 1 0 0 0 1 1 0 0 ( ) 2 1 3 1 2 1 3 3 c c c c c c x f x x − − − − = − − − − ◆ n阶行列式的计算

◆n阶行列式的计算 1 0 0 0 c4-33 1 1-x2 0 0 =-31-x2)(4-x2) 2 1 -3 0 2 -3 4-x2 求得fx)=0的根为x1=-1,x2=1,x3=-2,x4=2 (方法二)有性质2推论3知，当2-x2-1或9-x2=5时，f)=0. 故x=-1,x2=1,x3=-2,x4=2为fx)=0的根.由于fx)为x的 4次多项式，因此fx)=0只有4个根， n阶行列式的计算

n 阶行列式的计算 4 3 1 2 3 2 1 0 0 0 1 1 0 0 2 1 3 0 2 1 3 4 c c x x − − = − − − 2 2 = − − − 3(1 )(4 ) x x 求得f(x)=0的根为x1=-1，x2=1，x3=-2，x4=2 (方法二）有性质2推论3知，当2-x 2=1或9-x 2=5时，f(x)=0. 故x1 =-1，x2=1，x3 =-2，x4=2为f(x)=0的根.由于f(x)为x的 4次多项式，因此f(x)=0只有4个根. ◆ n阶行列式的计算

◆n阶行列式的计算 注：例3例4是利用行列式的性质2、5将行列式主 对角线下方的元素全化为零（即化为上三角行列式)， 行列式的值为主对角线上元素的连乘积. 由于化简过程具有程序化，因此工程技术上，常用计 算机程序计算高阶行列式的值 n阶行列式的计算

n 阶行列式的计算 注： 例3例4是利用行列式的性质2、5将行列式主 对角线下方的元素全化为零（即化为上三角行列式）， 行列式的值为主对角线上元素的连乘积. 由于化简过程具有程序化，因此工程技术上，常用计 算机程序计算高阶行列式的值. ◆ n阶行列式的计算