《线性代数》课程教学课件（PPT讲稿，C）n阶行列式的性质

第二节阶行列式的性质 卫 上页 返回

第二节 n 阶行列式的性质

课前复习：由定义知 01 012 13 D= 21 2 023 =01A1+012A2+a13Ag 31 L32 433 12 D- 2 Q2n : =a1A1+12A2+.+a1nAm . 上页

11 11 12 12 13 13 = + + a A a A a A 课前复习:由定义知 11 12 1 21 22 2 11 11 12 12 1 1 1 2 n n n n n n nn a a a a a a D a A a A a A a a a = = + + + 11 12 13 21 22 23 31 32 33 a a a D a a a a a a =

定理1.1.1n阶行列式可表示为如下形式 11 12 2 l22 ∑(-1m Pip2 Pn = ∑(-H)aa0n20, 回

定理1.1.1 n 阶行列式可表示为如下形式 ( 1 2 ) 1 2 1 2 1 2 ( 1) n n n t p p p p p np p p p = −  a a a n n nn n n a a a a a a a a a       1 2 21 22 2 11 12 1 ( 1 2 ) 1 2 1 2 1 2 ( 1) n n n t p p p p p p n p p p = −  a a a

练习：计算行列式D= 307 -5 1 302 解：由定义得 D=41A1+a12A12+13A13 =-3×(2)-5×0+3×7=27. D=a21A21+a22A22+L23A3 =04】+0x4。 =27. 上页

. 7 7 2 0 1 0 3 5 3 − − − D = 解: 由定义 得 ( ) 7 2 1 0 3 1 1 1 − = − − + = −3(− 2)− 50+ 37 = 27. ( ) ( ) 7 2 0 0 5 1 1+2 + −  − ( ) 7 7 0 1 3 1 2 2 − +  − + 练习: 计算行列式 D = a11A11 + a12A12 + a13A13 D a A a A a A = + + 21 21 22 22 23 23 21 =  0 A ( ) ( ) 2 2 3 3 1 1 7 2 + − + −  − 23 + 0 A = 27

一、行列式按行（列）展开法则 王 定理1.2.1：行列式等于它的任一行（列）的各元素 与其对应的代数余子式乘积之和，即 王王王王王王王王王王王 D-andn+ande++amdm-oad D=a4+4+.+arA=4 证明略。 (i=1,2,.,n) D=1An+a12A12+.+a1mA1n(i=1) =42421+22422+.+2m42n(i=2) =anlAnl+an24n2++aonAnn i-n

定理1.2.1: 行列式等于它的任一行(列)的各元素 1 n ki ki k a A = =  ( i =1, 2, ···, n) D = ai1Ai1 + ai2Ai2 + ··· + ainAin D = a1iA1i+ a2iA2i + ··· + aniAni 与其对应的代数余子式乘积之和, 即 一、行列式按行（列）展开法则 证明略。 1 n ik ik k a A = =  D = a11A11 + a12A12 + ··· + a1nA1n = a21A21 + a22A22 + ··· + a2nA2n = ···= an1An1 + an2An2 + ··· + annAnn ( i =1) ( i =2) ( i =n)

推论 一个n阶行列式，如果其中第i行所有 元素除外都为零，那末这行列式等于与它的 代数余子式的乘积，即D=a,A 11 L12 13 14 例如 D= L21 L22 L23 L24 0 0 33 0 041 L42 043 044 11 12 L14 =(-1) 33 21 u22 L24 041 L42 L44

推论 一个 阶行列式，如果其中第 行所有 元素除 外都为零，那末这行列式等于 与它的 代数余子式的乘积，即 D = aijA．ij n i aij aij 41 42 43 44 33 21 22 23 24 11 12 13 14 0 0 0 a a a a a a a a a a a a a D = ( 1) . 41 42 44 21 22 24 11 12 14 33 3 3 a a a a a a a a a a + = − 例如

二 行列式的性质 设 记 12 411 D 21 l22 D 22 : 0n2 m 行列式D'称为行列式D的转置行列式： 性质1.2.1行列式与它的转置行列式相等 回

二、行列式的性质 性质1.2.1 行列式与它的转置行列式相等. 行列式 D 称为行列式 的转置行列式.  D 设 nn a a a  22 11    n n a a a 2 12 1   1 2 21 n n a a a D =    2 21 1 n n a a a   n n a a a 1 2 12 ' D = nn a a a  22 11 记

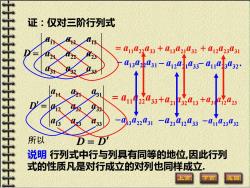
证：仅对三阶行列式 =011422033+41321032+012023431 413a22031-4124i4341103432 L让. 122g 0an4=4,☑，a。-4a,☑ 所以 说明行列式中行与列具有同等的地位，因此行列 式的性质凡是对行成立的对列也同样成立. 上页

11 21 31 12 22 32 13 23 33 a a a D a a a a a a  = 11 22 33 = a a a 11 23 32 −a a a 21 32 13 +a a a 31 12 23 +a a a 13 22 31 −a a a 21 12 33 −a a a 所以 D D =  11 22 33 = a a a . 11 23 32 − a a a 13 21 32 + a a a 12 23 31 + a a a 13 22 31 − a a a 12 21 33 − a a a 11 12 13 21 22 23 31 32 33 a a a D a a a a a a = 证：仅对三阶行列式 说明 行列式中行与列具有同等的地位,因此行列 式的性质凡是对行成立的对列也同样成立

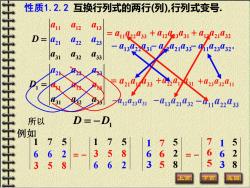
性质1.2.2互换行列式的两行（列），行列式变号 3 D L21 (73 112233+12g331+12132 13223T2133-i12332 31 032 33 22 +02332011 202331一13213 2-112033 所以 到9 7 7 5 6 58 16 6 6 2 3 528 136 56 5 528 5 3 回

11 12 1 2 31 32 1 22 23 3 33 a a a a a D a a a = a 21 22 2 1 31 32 3 3 11 12 13 3 a a a a a D a a a = a 11 22 33 −a a a 23 32 11 +aaa 13 21 32 −a a a 12 23 31 −a a a 22 13 31 +a a a 21 12 33 = a a a 11 22 33 = a a a . 11 23 32 − a a a 13 21 32 + a a a 12 23 31 + a a a 13 22 31 − a a a 12 21 33 − a a a 所以 D D = − 1 1 7 5 1 7 5 6 6 2 3 5 8 8 2 5 3 6 1 5 6 7 6 6 2 3 5 8 例如 = − 8 2 5 3 6 1 5 6 7 = − 性质1.2.2 互换行列式的两行(列),行列式变号

推论：如果行列式有两行（列）完全相同，则此行列式为零 证明：互换相同的两行，则有D=-D,所以D=0. 性质1.2.3：行列式的某一行（列）中所有的元素都乘以同一数k 等于用数乘此行列式 11 12 kai kai2 kain =k n ai2 Ani An2 Ann Anl an2 推论1：行列式的某一行（列）中所有元素的公因子可以提 到行列式符号的外面 推论2：行列式中如果有两行列)元素成比例，！ 则此行列 式为零

推论: 如果行列式有两行(列)完全相同, 则此行列式为零. 证明: 互换相同的两行, 则有D = – D, 所以D = 0. 性质1.2.3: 行列式的某一行(列)中所有的元素都乘以同一 数k, 等于用数k乘此行列式. n n nn i i in n a a a ka ka ka a a a          1 2 1 2 11 12 1 n n nn i i in n a a a a a a a a a k          1 2 1 2 11 12 1 = 推论1: 行列式的某一行(列)中所有元素的公因子可以提 到行列式符号的外面. 推论2: 行列式中如果有两行(列)元素成比例, 则此行列 式为零．