《线性代数》课程教学课件（讲稿，B）第二章_2.4矩阵的秩

2.4矩阵的秩 一、 矩阵的行（列秩、秩 矩阵秩与向量组的极 大 无关组、秩的求法 三、矩阵秩的第二定义 四、小结

§2.4 矩阵的秩 一、 矩阵的行(列)秩、秩 三、矩阵秩的第二定义 四、小结 二、 矩阵秩与向量组的极 大 无关组、秩的求法

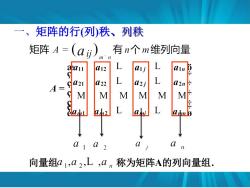
矩阵的行（列秩、列秩 矩阵A=(ai) 有n个m维列向量 u12 L arj a21 M2 L L A= M M M M M M L L 向量组a1,a2,L,a2称为矩阵A的列向量组

一、矩阵的行(列)秩、列秩 向量组 称为矩阵A的列向量组．

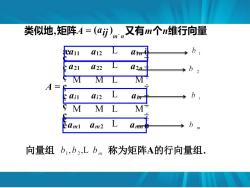
类{似地，矩阵A=(aj)mn又有m个维行向量 ea11 M12 421 M22 S M M M A= cail 4i2 M M M am2 L m 向量组b1,b2,Lb称为矩阵A的行向量组

向量组 称为矩阵A的行向量组．

1.定义2.4.1设mxn矩阵A,称A的行向量组的秩称 为矩阵A的行秩，列向量组的秩称为矩阵A的列秩 l016 例题1：求矩阵A=012的行秩和列秩 214 8 解：A的行向量a1=(1,0,1),a2=(0,1,2),43=(2,1,4) 101 由行列式012=0，知向量组a1,a2,43线性相关， 21

1.定义2.4.1 设m×n矩阵A，称A 的行向量组的秩称 为矩阵A的行秩，列向量组的秩称为矩阵A的列秩. 解：

又a1,M,线性无关，故a1,a,是A的行向量组的一个 最大无关组，所以矩阵A的行秩等于2. 同样方法可以求出A的列秩等于2. ®l1316 例题2：求矩阵A=c02-14的行秩和列秩. 80005每 解：A的三个行向量为 a1=(1,1,3,1),42=(0,2,-1,4),a3=(0,0,0,5). 去掉A的第三个分量量 ae=(1,1,1),a=(0,2,4),a=(0,0,5)

同样方法可以求出A的列秩等于2. 解：A的三个行向量为 去掉A的第三个分量量

111 由行列式024=1010，知向量组agaa线性无关 005 由§2.3例5知，向量组a1,42,03也线性无关， 所以A的行秩为3. 1ù 1ù e3ù 1ù A的列向量组b,=〉 b2= b4 eǘ 2ú e4ú 0日 0日 0日 51 4个三维向量必线性相关，而其中BBB,线性无关

4个三维向量必线性相关，而其中β1β2β4线性无关

因为 10 0 120=1010 145 所以A的列秩也等于3. 例1和例2中矩阵的行秩等于列秩并非是偶然的.为了 证明这一点，我们有以下两个定理. 2矩阵的初等行列变换对矩阵的行（列秩的影响。 定理2.4.1初等行（列变换不改变矩阵的行（列秩 证明：此处只就第三种初等行变换不改变矩阵的 行秩证明之，其余两种课下自己来完成

因为 所以A的列秩也等于3. 例1和例2中矩阵的行秩等于列秩并非是偶然的.为了 证明这一点,我们有以下两个定理. 定理2.4.1 初等行(列)变换不改变矩阵的行(列)秩. 证明： 此处只就第三种初等行变换不改变矩阵的 行秩证明之，其余两种课下自己来完成

设m'n矩阵A的行向量组a1,a2,L,am,且 1 ù 4 ú ú +ka ú A= i 4 =B ú e e ú eee 4 ú ú

由 a1=u1 LLL a;=(a;+kaj)-kaj LLL am-am 可知，矩阵A的行向量组可由B的行向量组线性表示. 显然，矩阵B的行向量组可由A的行向量组线性 表示.所以，矩阵A、B的行向量组等价.从而矩阵A、 B的行向量组的秩相同

可知，矩阵A的行向量组可由B的行向量组线性表示. 显然，矩阵B的行向量组可由A的行向量组线性 表示.所以，矩阵A、B的行向量组等价.从而矩阵A、 B的行向量组的秩相同

同样的方式可证明对矩阵做一次第二第三种类型 的初等行变换，可得到矩阵的行秩也相等D 定理2.4.1对应到化简线性方程组上即为初等变换不 改变线性方程组中独立方程的个数。 定理2.4.2初等行（列）变换不改变矩阵列（行）向量间 的线性关系. A=ana2,L ,an]b.b2,L,b,]=B 则有xa1+x02+L+x,4m=0 当且仅当xb1+x,b2+L+xbn=0

定理2.4.1对应到化简线性方程组上即为初等变换不 改变线性方程组中独立方程的个数。 定理2.4.2 初等行(列)变换不改变矩阵列(行)向量间 的线性关系