《线性代数》课程教学课件（PPT讲稿，C）矩阵的秩

第回 超件的线 1.行秩、列秩、矩阵的秩 2.矩阵秩的求法 3.向量组的秩的求法 4.矩阵秩的性质 5.矩阵秩与行列式的关系

1.行秩、列秩、矩阵的秩 2.矩阵秩的求法 3.向量组的秩的求法 4.矩阵秩的性质 5.矩阵秩与行列式的关系

2.4.矩阵的秩 1.行秩、列秩、矩阵的秩 把矩阵的每一行看成一个向量，则矩阵可被认为由这些行向量组成， 把矩阵的每一列看成一个向量，则矩阵可被认为由这些列向量组成。 定义2.4.1： 矩阵的行向量的秩，就称为矩阵的行秩； 矩阵的列向量的秩，就称为矩阵的列秩。 例如： 3 的行向量组是： 矩阵 0 2 -1 14 1=(1,1,3,1) A- 0 a2=(0,2,-1,4) 0 0 0 0 a3=(0,0,0,5) 4=(0,0,0,0)

2.4. 矩阵的秩 1. 行秩、列秩、矩阵的秩 把矩阵的每一行看成一个向量，则矩阵可被认为由这些行向量组成， 定义2.4.1：矩阵的行向量的秩，就称为矩阵的行秩; 矩阵的列向量的秩，就称为矩阵的列秩。 例如： 矩阵 1 1 3 1 0 2 1 4 0 0 0 5 0 0 0 0 A     − =         的行向量组是: 1 2 3 4 (1,1,3,1) (0,2, 1,4) (0,0,0,5) (0,0,0,0)     = = − = = 把矩阵的每一列看成一个向量，则矩阵可被认为由这些列向量组成

下面证明a1,02,x3是A的行向量组的一个极大无关组， 因为，由k1a1+k2a2+k3a3=0 即k,(1,1,3,1)+k2(0,2,-1,4)+k3(0,0,0,5) =(k1,k1+2k2,3k1-k2,k1+4k2+5k3) =(0,0,0,0) 可得k1=k2=k3=0,即a1,02,a3线性无关； 而4为零向量，包含零向量的向量组线性相关， .C1,02,03,C4线性相关。 王王 所以向量组a1,02,a3,C4的秩为3， 所以矩阵A的行秩为3。 上页

下面证明 1 2 3    , , 是A的行向量组的一个极大无关组， 因为，由 1 1 2 2 3 3 k k k    + + = 0 即 1 2 3 1 1 2 1 2 1 2 3 (1,1,3,1) (0,2, 1,4) (0,0,0,5) ( , 2 ,3 , 4 5 ) (0,0,0,0) k k k k k k k k k k k + − + = + − + + = 可得 1 2 3 k k k === 0, 即 1 2 3    , , 线性无关； 而  4 为零向量，包含零向量的向量组线性相关， 1 2 3 4     , 线性相关。 所以向量组 1 2 3 4     , 的秩为3， 所以矩阵A的行秩为3

矩阵A的列向量组是 1000 B. 120 3-0 45 0 0 111 由于 024H0≠0 005 所以B',B5,4 线性无关，即 B,B2,B4线性无关： 10 1 3 2 -1 而且 0 450 0 0 00 回

矩阵A的列向量组是 1 2 3 4 1 1 3 1 0 2 1 4 , , , 0 0 0 5 0 0 0 0                     − = = = =                                 即 1 2 4    , , 线性无关， 而且 1 1 3 1 0 2 1 4 0 0 0 0 5 0 0 0 0 − = 由于  111 0 2 4 10 0 005 ＝               = = =                    1 2 4 1 1 1 0 , 2 , 4 0 0 5    所以 1 2 4    , ,    线性无关

即B,B2,B3,B,线性相关， 因此向量组F,阝2，B3,B4的一个极大无关组是B,B2,B: 所以向量组B,2,B3,B,的秩是3， 所以矩阵A的列秩是3。 提出问题：矩阵的行秩 矩阵的列秩

因此向量组 1 2 3 4     , 的一个极大无关组是 1 2 4    , , 所以向量组 1 2 3 4     , 的秩是3， 所以矩阵A的列秩是3。 即 1 2 3 4     , 线性相关， 提出问题：矩阵的行秩 ? ＝ 矩阵的列秩

证明：矩阵的行秩=矩阵的列秩 定理2.4.1：矩阵的初等行变换不改变矩阵的行秩。 (列) (列) 证：把Amx,按行分块，设Amxm= &2 (1)对换矩阵A的两行 A的行向量组所含向量未变，所以向量组的秩不变， 所以矩阵A的行秩不变。 2)用非零常数k乘以A的第行 回

证明：矩阵的行秩＝ 矩阵的列秩 定理2.4.1：矩阵的初等行变换不改变矩阵的行秩。 （列） （列） 证：把 A m n 按行分块，设 1 2 m n m A         =       （1）对换矩阵A的两行   A的行向量组所含向量未变，所以向量组的秩不变， 所以矩阵A的行秩不变。 （2）用非零常数k乘以A的第i行

a1 A= ka =A, m 显然矩阵A的行向量组与A,的行向量组等价， 又等价的向量组有相同的秩， .A的行秩=A,的行秩， 即A的行秩不变

1 1 2 i kr i i m m A A k                   = ⎯⎯→ =                     显然矩阵 A 的行向量组与 A2 的行向量组等价， 又等价的向量组有相同的秩，  A 的行秩＝ A2 的行秩， 即A的行秩不变

(3)非零常数k乘以第行后加到第行上 显然，A,中的行向量组 i 可以由A的行向量组线性表示 4:4. -→ =A, aj+ka; 而A的行向量组可以由 A中的行向量组线性表示。 因而两个向量组等价，既行向量组的秩不变， 所以矩阵的行秩不变。 区回

（3）非零常数k乘以第i行后加到第j行上 1 1 3 i i i kr j j i m m A A k                              = ⎯⎯→ =         +             显然， A3 中的行向量组 可以由 A 的行向量组线性表示 而 A 的行向量组可以由 A3 中的行向量组线性表示。 因而两个向量组等价，既行向量组的秩不变， 所以矩阵的行秩不变

Th2.4.2:矩阵的初等行变换不改变矩阵的列向量间的线性关系。 (列) (行) 举例说明 12 例3设矩阵 1 4= 6 列向量组有线性关系 a4=41+2a2-a3 矩阵A经过有限次初等变换得到B,则矩阵B的 列向量B,P2,B,B,间也有线性关系 B4=B1+2B2-B3

Th2.4.2：矩阵的初等行变换不改变矩阵的列向量间的线性关系。 （列） （行） 举例说明 例3 设矩阵           = − 6 0 2 4 0 2 1 5 1 1 3 0 A 列向量组有线性关系 a4 = a1 + 2a2 − a3 矩阵A经过有限次初等变换得到B, 则矩阵B的 列向量 2 a 4 a3 a a1 , , , , 1  2  3  4 间也有线性关系  4 = 1 + 2 2 −  3

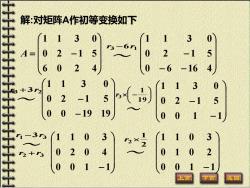
解：对矩阵A作初等变换如下 1 3 0 4- 0 2 5 2 -1 5 6 0 2 -6 -16 1 1 3 +3r2 1 1 1 3 0 2 0 -1 0 0 19 19 0 0 1 -1 1 1-2 1 0 3 0 2 0 0 1 0 2 001 0 0 返回

解:对矩阵A作初等变换如下           = − 6 0 2 4 0 2 1 5 1 1 3 0 A           − − − 0 6 16 4 0 2 1 5 1 1 3 0 r3 6r1 ～ − r3 3r2 ～ +           − − 0 0 19 19 0 2 1 5 1 1 3 0        − 19 1 3 r ～           − − 0 0 1 1 0 2 1 5 1 1 3 0 1 3 2 3 r 3r r ～ r − +           0 0 1 − 1 0 2 0 4 1 1 0 3 2 1 r2  ～           0 0 1 − 1 0 1 0 2 1 1 0 3