《高等数学》课程教学资源（课件讲稿）第一章 函数与极限_1-3 函数极限

第三节 断数的极限 一、函数极限的概念 二、函数极限的性质

二、 函数极限的性质 一 、函数极限的概念 第三节 函数的极限

(一)函数极限的概念 数列{x}的极限可以看作自变量为正整数的函数： xn=f(m),n∈N+当n→+oo时的极限， Xn X2 0 0 0 0

（一）函数极限的概念 1 x 1 2 x 2 3 x 3 n x . . n . . 0 xn n ( ), n x f n n N n      当 时的极限. 数列 { } 的极限可以看作自变量为正整数的函数: n x

(一) 函数极限的概念 对y=f(x),自变量变化过程的六种形式： (1)x→x (2)x→x 5)x→ +0 (3)x→x, (6x→-0

（一）函数极限的概念 0 ( 1 ) x x  0 ( 2 ) x x   0 ( 3 ) x x   ( 4 ) x   ( 5 ) x    ( 6 ) x    自变量变化过程的六种形式:

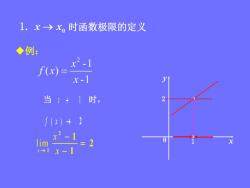
1.x→x。时函数极限的定义 ◆例： x2-1 f(x)= x-1 当】1时， 2 f(x)→2 2 x-1 lim =2 x→1X-1

0 x y 例： 1 当 2 x  1 时， f x ( )  2 lim 2 1 1 2  1   x  x x 1. 时函数极限的定义

定义1，设函数f(x)在点x的某去心邻域内有定义， 若6>0,36>0，当00,36>0,当x∈U(xo,8) x→x0 时，有f(x)-A<6 几何解释： y=f(x) A+8 A-8 O,-6x0,+0X

定义1 . 设函数 在点 的某去心邻域内有定义 ,    0 ,    0 , 当     0 0 x x 时, 有 f ( x )  A   则称常数 A 为函数 当 时的极限, f x A x x   lim ( ) 0 或 即 当 时, 有 若 记作 A   A   几何解释: O A 0 x   0 x0 x   x y y  f ( x )

例1.证明limC=C(C为常数) x→xo 证： f(x)-A=C-C=0 故V6>0,对任意的6>0，当0<x-x0<8时， 总有 C-C=0<8 因此 lim C=C x→x0

例1. 证明 证: f ( x )  A 故    0 , 对任意的   0 , 当 时 , 因此 总有

例2.证明 lim(2x-1)=1 x→I 证：f(x)-A=(2x-1)-1=2x-1 Ve>0,欲使fx)-A<c,只要x-1<2, 取6=2，则当0<x-1k6时，必有 f(x)-A=(2x-1)-1<8 因此 lim(2x-1)=1 x-→1

例2. 证明 证:  2 x  1    0 , 欲使 取 , 2    则当 0  x  1   时, 必有 因此 只要

例3.证明i x2-1 =2 >1x-1 证：f(x)-A x2-1 -2 =x+1-2=x-1 x-1 故Ve>0.取δ=6，当0<x-1<8时，必有 x2-1 -2 <8 x-1 x2-1 因此 lim* =2 x→1x-1

例3. 证明 证: f ( x )  A 故    0 , 取    , 当 时, 必有      2 1 1 2 x x 因此 2 1 1 lim 2 1     x x x

例4.证明：当xo>0时limx=xo: x→x0 证：f(x)-A=Vx-Vx0 x-x0 x+xo VE>0,欲使f(x)-A<6,只要x-x<Vx6,且 x≥0.而x≥0可用x-x0≤x保证.故取 6=min{√xs,xo},则当0<x-xgk6时，必有 x-√ 0≤8 因此 limx=√xo x→x0

例4. 证明: 当 证: 0 0 1 x x x      0 , 欲使 且 而 可用 因此 只要 0 0 lim x x x x   时 故取 m in  ,  , 0 0   x  x 则当     0 0 x x 时, 保证 . 必有 O x x0

2.x→x时单侧极限的定义 x2-1 ◆例： f(x)= x-1 当x→1时，f(1)=2 2 x2-1 lim =2 x→1° x-1 当x>1时，f(1)=2 →1 x2-1 lim =2 x→1*X-1

例： 当 x   1 时， f ( )  1 2  lim x x x      2 1 1 2 1 2. 时单侧极限的定义 当 x   1 时， f ( )  1 2  lim x x x      2 1 1 2 1 0 x y 1 2 x   1 x   1