《高等数学》课程教学资源（课件讲稿）第三章 微分中值定理与导数的应用_3-6 函数图形的描绘

第之节 第三章 岛数周形的描羚 一、 曲线的渐近线 二、函数图形的描绘

第六节 一、 曲线的渐近线 二、 函数图形的描绘 函数图形的描绘 第三章

曲线的渐近线 1.水平与铅直渐近线 若limf(x)口b,则曲线y口f(x)有水平渐近线y口b, x口O□ (或x口□) 若imf(x)口口，则曲线y口f(x)有铅直渐近线x口x。 x口对 (或x口) 例1.求曲线y 口2的渐近线 x☐ 解：口lim( ▣2)口2 x0口x□1 口y口2为水平渐近线 lim(2)口口，口x1为铅直渐近线 x01x▣1

1. 水平与铅直渐近线 若 则曲线 有水平渐近线 若 则曲线 有铅直渐近线 例1. 求曲线 的渐近线 . 解: 为水平渐近线; 为铅直渐近线. 一、 曲线的渐近线

2.斜渐近线 若lim[f(x)口(kx□b)]□0，则曲线y☐f(x)有 x0□ (或x口□) 斜渐近线y口kx口b lim[f(x)▣(k.x回b)]口0 x口O klim x口□ x国O k☐lim xx (或x口D) b▣lim[f(x)□kx] x口 xO口 (或x口▣)

2. 斜渐近线 斜渐近线 若

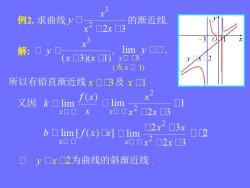
.3 例2.求曲线y口 的渐近线， ▣2x口☐3 解：口y口 limy口▣， (x口3)x☐I) x口B (或x▣1) 所以有铅直渐近线x口3及x口1 又因k▣lim f(x) lim 01 x口口X x0口x2☐2x☐3 □2x2☐3x b▣lim[f(x)Cx]▣lim ▣2 x口□ x00x2□2x□3 口y口x☐2为曲线的斜渐近线

例2. 求曲线 的渐近线. 解: 所以有铅直渐近线 及 又因 为曲线的斜渐近线

练习.求曲线 的斜渐近线

练习. 求曲线 的斜渐近线

二、函数图形的描绘 步骤： 1.确定函数y口f(x)的定义域，并考察其对称性及周 期性； 2.求fCx),f),并求出fx)及fx)为0和不存在 的点； 3.列表判别增减及凹凸区间，求出极值和拐点； 4.求渐近线； 5.确定某些特殊点，描绘函数图形

二、函数图形的描绘 步骤 : 1. 确定函数 的定义域 , 期性 ; 2. 求 并求出 及 3. 列表判别增减及凹凸区间 , 求出极值和拐点 ; 4. 求渐近线 ; 5. 确定某些特殊点 , 描绘函数图形 . 为 0 和不存在 的点 ; 并考察其对称性及周

例3.描绘y口x3☐x2口2的图形 解：1)定义域为（口，口口），无对称性及周期性 2)y0中x202x,y2x2 令y血0，得x口0,2 令y□0，得x口1 01 23x 3) (，0) 0 (0,1)11,2)2(2,▣▣) yl y[ 4 2 3 23 01 (极大) (拐点) (极小) 3 2

例3. 描绘 的图形. 解: 1) 定义域为 无对称性及周期性. 2) 3) (极大) (拐点) (极小) 4)

例4.描绘方程(x☐3)2☐4y☐4xy口0的图形 解：10yx03)2 定义域为（口，1），(1，口▣)》 4(x☐1)1 2)求关键点.原方程两边对x求导得 2(x☐3)☐4y☐4y☐4xy▣0 ① 323)xG) 2(x☐1) 4(x☐1)2 @两边对x求导得 204yI☐8y☐4xy☐0 x1040 2 2(x☐1)(x01)1 令y中0得x口□l,3:

例4. 描绘方程 的图形. 解: 1) 定义域为 2) 求关键点. 原方程两边对 x 求导得 ① ①两边对 x 求导得

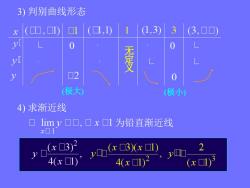
3)判别曲线形态 (D,1) 01 (☐，1)1 1,3) 3 (3,▣ 0 0 无定义 02 (极大 (极小) 4)求渐近线 口limy口口，口x口1为铅直渐近线 x▣1 v 3) 2 4(x☐1)2 (x☐1)3

3) 判别曲线形态 (极大) (极小) 4) 求渐近线 为铅直渐近线 无 定 义

又因 即明 b口1imy0x)a1imrx3) x0▣4 x▣口4(x☐1)4 □5x□9 ▣lim x0▣4(x☐1) 4 y0(x03)2 4(x☐1) 5 x口，为斜渐近线 4 y3)(x G) 4(x☐1)2 5)求特殊点 0 2 9 1 2 4 4 (x☐)3

又因 即 5) 求特殊点 为斜渐近线