《高等数学》课程教学资源（课件讲稿）第五章 定积分_5-1 定积分的概念与性质

第一节 第五章 定积分的桡念及性质 一、 定积分问题举例 二、 定积分的定义 三、定积分的性质

第一节 一、定积分问题举例 二、 定积分的定义 定积分的概念及性质 第五章 三、 定积分的性质

一、定积分问题举例 矩形面积口ah h 梯形面积口二(a☐b) 2 1.曲边梯形的面积 设曲边梯形是由连续曲线 y口f(x)(f(x)☐0) 及x轴，以及两直线x口a,x口b A▣？ 所围成，求其面积A b x

一、定积分问题举例 1. 曲边梯形的面积 设曲边梯形是由连续曲线 以及两直线 所围成 , 求其面积 A . 矩形面积 梯形面积

解决步骤： 1)分割.在区间[a,b]中任意插入n-1个分点 a口x0口□x2□0□xn0☐xn☐b 用直线x口x,将曲边梯形分成n个小曲边梯形 2)取近似.在第i个窄曲边梯形上任取口□[xa,x,] 作以[x和，x,为底，f(口) 为高的小矩形，并以此小 矩形面积近似代替相应 窄曲边梯形面积口4，得 a x 口4，□f(g)☐x,(x,Dx,口xa)

解决步骤 : 1) 分割. 在区间 [a , b] 中任意插入 n –1 个分点 用直线 将曲边梯形分成 n 个小曲边梯形; 2) 取近似. 在第i 个窄曲边梯形上任取 作以 为底 , 为高的小矩形, 并以此小 矩形面积近似代替相应 窄曲边梯形面积 得

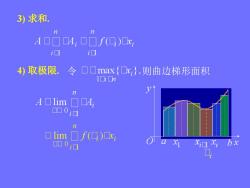
3)求和 n A口☐ū4,0口f(0)Dx, i▣ ▣ 4)取极限.令口口ax{口x},则曲边梯形面积 1☐i0n 之 A▣1im☐☐4 0000 n lim 1口f(g)Dx, 0001

3) 求和. 4) 取极限. 令 则曲边梯形面积

2.变速直线运动的路程 设某物体作直线运动，己知速度v口v(t)口C[T,T2],且 v(t)口0，求在运动时间内物体所经过的路程s. 解决步骤： 1)分割.在[T,T2]中任意插入n口个分点，将它分成 n个小段[ta,t;](i□1,2，口，n),在每个小段上物体经 过的路程为口s,(i☐1,2，☐，n) 2)取近似.任取口口[t0,t],以v(g)代替变速，得 □s,□v(g)t,(i☐1,2，☐，n)

2. 变速直线运动的路程 设某物体作直线运动, 且 求在运动时间内物体所经过的路程 s. 解决步骤: 1) 分割. 将它分成 在每个小段上物体经 2) 取近似. 得 已知速度 n 个小段 过的路程为

3)求和. n s▣□v(C)回t i▣ 4)取极限， n s▣lim☐v(C)□t (口▣max☐t:) 000 ia 1▣i☐n 上述两个问题的共性 ·解决问题的方法步骤相同： “分割，取近似，求和，取极限” ·所求量极限结构式相同：特殊乘积和式的极限

3) 求和. 4) 取极限 . 上述两个问题的共性: • 解决问题的方法步骤相同 : “分割 , 取近似 , 求和 , 取极限 ” • 所求量极限结构式相同: 特殊乘积和式的极限

二、定积分定义P226 a口x0口x□x2□0□xn口b

二、定积分定义 (P226 )

则称此极限I为函数f(x)在区间[a,] 上的定积分，记作f(x)dx n 即 f(x)dx lim口f(q)0x, 00d 此时称f(x)在[a,b]上可积

则称此极限 I 为函数 在区间 上的定积分, 即 此时称 f ( x ) 在 [ a , b ] 上可积 . 记作

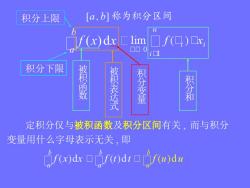
积分上限 [a,b]称为积分区间 f(x)dx lim f() 0▣0 积分下限 被积函数 被积表达式 积分变量 积分和 定积分仅与被积函数及积分区间有关，而与积分 变量用什么字母表示无关，即 rx)dr口f0dufw)dm

积分上限 积分下限 被 积 函 数 被 积 表 达 式 积 分 变 量 积 分 和 定积分仅与被积函数及积分区间有关 , 而与积分 变量用什么字母表示无关 , 即

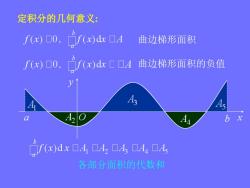
定积分的几何意义： f(x)☐0，f(x)dxDA 曲边梯形面积 f(x)口0，□f(x)dxC☐.A 曲边梯形面积的负值 7f(x)dx040.4,☐4口4，□4 各部分面积的代数和

定积分的几何意义: 曲边梯形面积 曲边梯形面积的负值 各部分面积的代数和