《高等数学》课程教学资源（PPT课件）第三章 微分中值定理与导数的应用_3-2 洛必达法则

第二节 洛必达法则 8 型未定式 二、”型未定式 00 三、其他未定式

三、其他未定式 二、 型未定式 一、 型未定式 0 0 第二节 洛必达法则

本节研究： 函数之商的极限im (x) 0 ( 或”型 8(x) 0 转化 洛必达法则 导数之商的极限1im f'(x) g'(x)

函数之商的极限 导数之商的极限 转化 ( 或 型) 本节研究: 洛必达法则 洛必达

型未定式 0 定理1. 1)lim f(x)=lim F(x)=0 x→ x->a 2)f(x)与F(x)在U(a)内可导，且F'(x)≠0 lim 3) "C) 存在（或为0）》 x→aF'(x) lim f(x) lim f() x-aF(x） xa F'(x) (洛必达法则)

一、 ( ) ( ) 3) lim F x f x x a   → 存在 (或为 ) ( ) ( ) lim ( ) ( ) lim F x f x F x f x x a x a   = → → 2) f (x)与F(x) 在U (a)内可导,  定理 1. 型未定式 0 0 (洛必达法则)

洛必达法则 lim f(x) = lim (x) →aF(x aF'(x） 推论1.定理1中x→a换为下列过程之一 x→a，X→a,x→0，x→+0，x→-0 条件2)作相应的修改，定理1仍然成立 推论2若m 仍属。型，且/).F(满足定 理1条件，则 lim f()=lim f)=lim f"(x) F(x) F'(x) F"(x)

推论1. 定理 1 中 x → a 换为下列过程之一: , → − x a 推论 2. 若 ( ) ( ) lim F x f x   理1条件, 则 条件 2) 作相应的修改 , 定理 1 仍然成立. x → +, 洛必达法则 定理1

x3-3x+2 0 例1.求m 型 1x3-x2-x+1 3 0 解：原式 海m 3x2-3 x→1 3x2-2x-1 逢 6x 3 lim x>16x-2 2 注意：不是未定式不能用洛必达法则！ 6x li ≠lm。=l x→16x-2 x-→16

例1. 求 解: 原式 型 0 0 2 3 = 注意: 不是未定式不能用洛必达法则 ! 6 2 6 lim →1 x − x x 1 6 6 lim 1 =  x→ 3 3 2 x − 3 2 1 2 x − x − lim →1 = x 洛 6 2 6 lim 1 − = → x x x 洛

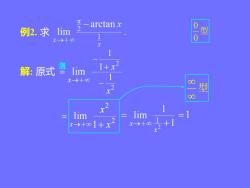
-arctanx 例2.求1im 2 0 型 x>+00 1 0 X 解：原式 lim 1+x 1 X>+0 00 x2 型 o lim lim x→+∞1+x1

例2. 求 解: 原式 →+ = x lim 型 0 0 2 2 1 lim x x x + = →+ =1 2 1 1 + x − 2 1 x − 1 1 lim 2 1 + = →+ x x 型   洛

00 二、 型未定式 00 定理2. 1）limf(x)y=limF(x)=∞ x→a x->a ● 2)f(x)与F(x)在U(a)内可导，且F'(x)≠0 3) lim I') 存在（或为∞） x→aF'(x) lim f(x) = lim f'(x) (洛必达法则 aF(x） x-a F'(x)

二、   型未定式 ( ) ( ) 3) lim F x f x x a   → 存在 (或为∞) ( ) ( ) lim F x f x x→a 定理 2. ( ) ( ) lim F x f x x a   = → (洛必达法则) 2) f (x)与F(x) 在U (a)内可导, 

说明：定理中x→a换为 x->a, x->a, X→0， X>十0， X→-0 之一，条件2)作相应的修改，定理仍然成立 足理

说明: 定理中 x → a 换为 之一, 条件 2) 作相应的修改 , 定理仍然成立. , → + x a , → − x a x → , x → +, x → − 定理2

例3.求 lim Inx (n>0) 00 x-→+0xn 型 解： 原式=lim lim =0 x→+0.nx 例4.求lim x” 00 (n>0,2>0) 型 -→to∞e 0 解 原式=lim nx-I lim n(n-1)xm-2 X->+00 X→+00 22e2x 喧.道 lim n. X>+0 r=0

例3. 求 解: 原式 1 1 lim − →+ = n x x nx n x nx 1 lim →+ = = 0 例4. 求 解: 原式 = 0 x n x nx   e lim −1 →+ = x n x n n x   e ( 1) lim 2 −2 →+ − = ( 0). e lim   →+   n 0 , x x n x 型   型   洛 n x x n   e ! lim →+ = = 洛 洛

说明： 1)例3，例4表明x→+0时， Inx, x"(n>0),e2x(2>0) 后者比前者趋于+∞更快 2)在满足定理条件的某些情况下洛必达法则不能解决 计算问题.例如 用洛必达法则 /1+x1 W1+x2 lim lim lim X->+00 X x→+01+ X→十0 X V1+x2 事实上 lim lim /2+1=1 x-→+00

例4. 0 ( 0). e lim =   →+   n 0 , x x n x 0 ( 0). ln lim =  →+ n x x n x 例3. 说明: 1) 例3 , 例4 表明 x → + 时, ln x, 后者比前者趋于 +  更快 . 例如, 事实上 e (  0) x 用洛必达法则 2) 在满足定理条件的某些情况下洛必达法则不能解决 计算问题