《高等数学》课程教学资源（PPT课件）第三章 微分中值定理与导数的应用_3-3 泰勒公式

第三节泰勒公式 一、泰勒公式的建立 二、几个初等函数的麦克劳林公式 三、泰勒公式的应用

二、几个初等函数的麦克劳林公式 第三节 一、泰勒公式的建立 三、泰勒公式的应用 泰勒公式

一、泰勒公式的建立 在微分应用中已知近似公式 f(x)≈f(x)+f'(x(x-x) y=f(x) P(x) P(x -x)的一次多项式 特点乃(xo)=f(xo） Xo x 以直代曲 Pi(xo)=f(xo) 如何提高精度？ 需要解决的问题 如何估计误差？

特点: ( ) 0 = f x ( ) 0 = f  x 一、泰勒公式的建立 f ( x) ( ) ( ) ( ) 0 0 0  f x + f  x x − x 以直代曲 0 x ( ) 1 p x 在微分应用中已知近似公式 : 需要解决的问题 如何提高精度 ? 如何估计误差 ? x (x-x0 )的一次多项式 x y y = f ( x) O

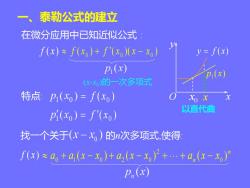
一、泰勒公式的建立 在微分应用中已知近似公式 f(x)≈f(x)+∫'(x(x-x） y=f(x) Pi(x) P(x) (x-x)的一次多项式 特点：卫(xo)=f(xo) Xo x p(xo)=f(xo) 以直代曲 找一个关于(x-x,)的n次多项式使得 f(x)≈a+a1(x-x)+a(x-x+.+an(x-x) B,(x)

特点: ( ) 0 = f x ( ) 0 = f  x 一、泰勒公式的建立 f ( x) ( ) ( ) ( ) 0 0 0  f x + f  x x − x 以直代曲 0 x ( ) 1 p x 在微分应用中已知近似公式 : x (x-x0 )的一次多项式 x y y = f ( x) O 找一个关于 的n次多项式,使得: f ( x) 2 0 1 0 2 0 0 ( ) ( ) ( ) n n  + − + − + + − a a x x a x x a x x

1.求n次近似多顶式pn(x),要求： Pn(xo)=f(xo)h(xo)=f"(xo), (xo)=f(xo) Pn(x)=a0+a1(x-x0)+a2(x-x0)广+.+amn(x-xo) 则 ph(x)= 4+2a2(x-x0)+.+nan(x-x0)m- ph(x)= 2!a2+.+n(n-1)an(x-x0)-2 p"(x)= nlan ao=Pn(xo)=f(xo), a pn(xo)=f'(xo), 2=P(x)=f"(xo).,an=aP(xg)=f(x》 故Pta,对t(%xxx件. +了(p对0

f ( x) 2 0 1 0 2 0 0 ( ) ( ) ( ) n n  + − + − + + − a a x x a x x a x x 1. 求 n 次近似多项式 要求: ( ) 2! 0 1 2 a p x n =  ( ), 0 = f  x  , ( ) 0 ( ) ! 1 a p x n n = n n ( ) 0 ( ) f x n = 故 pn (x) = ( ) 0 f x ( )( ) 0 0 + f  x x − x +  2! 1 ! 1 n n n f (x )(x x ) 0 0 ( ) + − ! 1 n 2 0 0 + f (x )(x − x ) 2! 1 pn (x) = 则 pn  (x) = pn (x) =     n p (n) (x) = n!a n ( ) 0 0 a p x = n ( ), 0 = f x ( ) 1 0 a p x n =  ( ), 0 = f  x a1 2 ( ) 2 0 + a x − x 1 0 ( ) − + + − n n  n a x x 2 2 !a 2 0 ( 1) ( ) − + + − − n n  n n a x x a0 n n a ( x x ) a (x x ) a (x x ) 0 2 + 1 − 0 + 2 − 0 + + −

泰勒(Taylor)中值定理： 若f(x)在包含x的某开区间(a,b)内具有 直到n+1阶的导数，则当x∈(a,b)时，有 f)=j0)+,0x-)+'2x-w2+ 21 (x-x)"+R(x) ① n! 其中Rn(x)= +(5 (n+1)1 (x-x)m(5在x与x之间)② 公式①称为f(x的n阶泰勒公式 公式②称为n阶泰勒公式的拉格朗日余项

公式 ① 称为 的 n 阶泰勒公式 . 公式 ② 称为n 阶泰勒公式的拉格朗日余项 . 泰勒(Taylor)中值定理 : 阶的导数 , 时, 有 ( ) 0 f x ( )( ) 0 0 + f  x x − x 2 0 0 ( ) 2 ! ( ) x x f x −  + +  n n x x n f x ( ) ! ( ) 0 0 ( ) + − R (x) + n ① 其中 1 0 ( 1) ( ) ( 1)! ( ) ( ) + + − + = n n n x x n f R x  ② 则当 ) 0 ( 在 x 与 x 之 间 泰勒

注意到 Rn(x)=o[(x-xo)”] ③ 在不需要余项的精确表达式时，泰勒公式可写为 f)-f)+f()-x)+(x-x+. 2 +(2x-》”+x-x0)1 n! 公式③称为n阶泰勒公式的佩亚诺Peano)余项 *可以证明 f(x)在点o有直到n阶的导数 ④式成立

公式 ③ 称为n 阶泰勒公式的佩亚诺(Peano) 余项 . 在不需要余项的精确表达式时 , 泰勒公式可写为 f (x0 ) + f ( x0 )(x − x0 ) 0 ( 0 ) 2 +  2 ! ( ) x x f x −  + n n x x n f x ( ) ! ( ) 0 0 ( ) + − [( ) ] 0 n + o x − x ( ) [( ) ] 0 n n 注意到 R x = o x − x ③ ④ * 可以证明: ④ 式成立

f(x)=f(xo)+f(xox-x)+(xx+. 21 n (n+1) 特例： (5在x与x之间) (1)当n=0时，泰勒公式变为 拉格朗日中值定理 f(x)=f(xo)+f'()(x-xo) (5在x,与x之间)》 (2)当n=1时，泰勒公式变为 )=f+fx-x+(x-,月 2! 可见f(x)≈f(x,)+'(xo)x-xo) (5在x与x之间) 误差 R=2(x-尸（传在xn与x之间 df 21

特例: (1) 当 n = 0 时, 泰勒公式变为 f (x) = ( ) 0 f x ( )( ) 0 + f   x − x (2) 当 n = 1 时, 泰勒公式变为 拉格朗日中值定理 f (x) = ( ) 0 f x ( )( ) 0 0 + f  x x − x 2 0 ( ) 2 ! ( ) x x f −  +  可见 误差f (x) = ( ) 0 f x ( )( ) 0 0 + f  x x − x +  1 0 ( 1) ( ) ( 1)! ( ) + + − + + n n x x n f  2 0 0 ( ) 2 ! ( ) x x f x −  + n n x x n f x ( ) ! ( ) 0 0 ( ) + − d f ) 0 ( 在 x 与 x 之 间) 0 ( 在 x 与 x 之 间 ) 0 ( 在 x 与 x 之 间 ) 0 ( 在 x 与 x 之 间

在泰勒公式中若取x。=0,记5=0x(0<0<1),则有 f=f0+/ox+0x2++f0 21 n f(0x) n+l (n+1) 称为麦克劳林(Maclaurin)公式， 由此得近似公式 fx)sf0)+0x+0x2++0x 2! n! 若在公式成立的区间上fm+”(x)≤M,则有误差估计式 R(x)i5- M

称为麦克劳林( Maclaurin )公式 . 0, x0 = 则有 f (0) + f (0) x 2 +  2 ! (0) x f  + n n x n f ! (0) ( ) + 在泰勒公式中若取 f (x) = ( ) 0 f x ( )( ) 0 0 + f  x x − x +  1 0 ( 1) ( ) ( 1)! ( ) + + − + + n n x x n f  2 0 0 ( ) 2 ! ( ) x x f x −  + n n x x n f x ( ) ! ( ) 0 0 ( ) + − ) 0 ( 在 x 与 x 之 间 f (x)  f (0) + f (0) x +  ( ) , ( 1) f x M n  + 则有误差估计式 1 ( 1)! ( ) + +  n n x n M R x 2 2 ! (0) x f  + n n x n f ! (0) ( ) + 若在公式成立的区间上 麦克劳林 由此得近似公式 记  =  x (0    1)

二、几个初等函数的麦克劳林公式 (1)f(x)=e f0(x)=e,f(0)=1(k=1,2,） e*=1+x+* 131 .++R,（ n! 其中 R(x)= x+ (0<0<1) (n+1)！ 80w+940re 麦克劳林公式 x n! (n+1) (0<0<1)

二、几个初等函数的麦克劳林公式 ( ) e , (k ) x  f x = (0) 1 ( 1, 2 , ) f (k ) = k =  x  e = 1 + x 3! 3 x + +  n! x n + R (x) + n 2! 2 x + 其中 f (0) + f (0) x 2 +  2 ! (0) x f  + n n x n f ! (0) ( ) + 麦克劳林公式 (0    1)

(2)f(x)=sinx sin e=a经{8w k =2m (m=1,2,.） .sinx=x 2m-1 31+51m+(- (2m-1)1 R2m(x) 其中Rm(x)= (-1)"cos(0x) x2m+1 (0<0<1) (2m+1) 麦克劳林公式 /=7of0r+0x+.+0x+/a0xH 21 n! (n+1)I (0<0<1)

sin( π ) 2 2 +1 + m ( 1) xcos( x) m −  ( ) = sin(x + ) ( ) f x k   sin x = x 3! 3 x − 5! 5 x + (2 1)! 2 1 − + − m x m ( ) 2 R x + m 其中 R2m (x) = 2 π k  2 π (0) sin ( ) f k k =    = 0, k = 2m ( 1) , k = 2m −1 −1 − m (m = 1, 2 , ) −  1 ( 1) − − m (0    1) 2m+1 x (2m +1)! f (0) + f (0) x 2 +  2 ! (0) x f  + n n x n f ! (0) ( ) + (0    1) 麦克劳林公式