《高等数学》课程教学资源（课件讲稿）第二章 导数与微分_2-2 求导法则

第二节 岛数的求导法则 一、 四则运算求导法则 二、反函数的求导法则 三、复合函数求导法则 四、初等函数的求导问题

第二节 二、反函数的求导法则 三、复合函数求导法则 四、初等函数的求导问题 一、四则运算求导法则 函数的求导法则

解决求导问题的思路： fx)▣lim f(x口口x)口f(x) 构造性定义) 口x▣0 ■ 本节内容 求导法则 (C)中0 (sinx)▣ coSx 证明中利用了 (nx)西 其他基本初等 两个重要极限 函数求导公式 初等函数求导问题

解决求导问题的思路: ( 构造性定义 ) 求导法则 其他基本初等 函数求导公式 证明中利用了 两个重要极限 初等函数求导问题 本节内容

一、四则运算求导法则 定理1.函数口(x)及v□v(x)都在点x可导 →(x)及v(x)的和、差、积、商（除分母 为O的点外)都在点x可导，且 (1)[(x)☐v(x)]Dux)口vCx) (2)[u(x)v(x)]☐ux)v(x)☐u(x)vx) (3 gu(四aGD(wp (v(x)☐0） 目v(x)E v-(x) 下面分三部分加以证明，并同时给出相应的推论和 例题

一、四则运算求导法则 定理1. 的和、差、积、商 (除分母 为 0的点外) 都在点 x 可导, 且 下面分三部分加以证明, 并同时给出相应的推论和 例题

(1)(w☐v)Du☐v0 证：设f(x)口u(x)☐v(x),则 fqx)口lim f(x☐h)☐f(x) h▣0 h lim [u(x☐h)☐v(xDh)]□[u(x)☐v(x)] h☐0 h u(x☐h)☐u(x) ▣lim lim v(x☐h)☐v(x) h▣0 n h▣0 h 口ux)☐vx) 故结论成立， 此法则可推广到任意有限项的情形.例如， (u☐y☐P)DDv☐

此法则可推广到任意有限项的情形. 证: 设 则 故结论成立. 例如

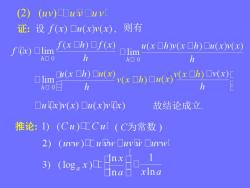
(2) (uy)☐更u☐uy 证：设f(x)口u(x)v(x),则有 fx)☐lim f(x□h)▣f(x) u(x☐h)v(x☐h)☐u(x)v(x) ▣lim h▣0 h h▣0 ▣lim 2(x☐h)☐u(x) 0日 (xCh)☐(x)'x☐h(xU n ☐ux)v(x)☐u(x)vx） 故结论成立 推论：1)(Cu)工Cu[(C为常数) 2)(1w)工u☐1v☑☐1w[ 3)(loga x)口 nx Ina xlna

(2) 证: 设 则有 故结论成立. 推论: ( C为常数 )

例1.y☐Vx(x3☐4cosx☐sinl),求y及ya 解：y中(x)I(x3口4cosx☐sin1)》 ☐(x3☐4cosx☐sinl)[ 巴(4 cosinl)正x(3x4simx7 (4cosin1)(34sin1) 77 □-口sinl□2cosl 2 2

例1. 解:

(3) Ouvt 2 y2 证：设f(x)C ，则有 u(x) u(x▣h) (x f()lim f(x□h)口f(x) lim v(x☐h v(x) h▣0 h h▣0 h n(x☐h)☐uxv(x)☐u(x) v(x☐h)☐(x) ▣lim h h h00 v(x☐h)v(x) ux)v(x)☐u(x)vx) 故结论成立， v-(x) 推论： 3 (C为常数)

(3) 证: 设 则有 故结论成立. 推论: ( C为常数 )

例2.求证(tanx)☐sec2x,(cscx)☐☐cscxcotx. 证 (tanx)▣ (sinx)cosx sinx(cosx) coSx CoS-x ☐sinx ☐secx cos-x ☐(sinx)l Lcos x (cscx) sin x sinx sinx ▣□cscxcotx 类似可证：(cotx)卫□csc2x,(secx)☐sec xtanx

例2. 求证 证: 类似可证:

二、反函数的求导法则 定理2.设y口f(x)为x口f口(y)的反函数，f口(y)在 y的某邻域内单调可导，且[f口(y]四0之 或 d x d v 证：在x处给增量口x口0，由反函数的单调性知 D/(x0)0f(x)00,口D1 且由反函数的连续性知☐x口0时必有☐y口0，因此 fqx)▣lim ▣lim 1 DxD0□x [f)]

二、反函数的求导法则 定理2. y 的某邻域内单调可导, 证: 在 x 处给增量 由反函数的单调性知 且由反函数的连续性知 因此

例3.求反三角函数及指数函数的导数， 解：1)设y□arcsinx,则x□siny,y口（□ 2 2 cosy口0，则 (arcsinx)[☐ (sin y) coS y /1sin2y V1x3 利用 arccosx)T☐ arccosx ☐arcsin x /1□x 2 类似可求得 (arctanx) 1x3 (arccotx) 10x2

例3. 求反三角函数及指数函数的导数. 解: 1) 设 则 类似可求得 利用 , 则