《高等数学》课程教学资源（课件讲稿）第四章 不定积分_4-2 换元积分法

第二为 第四章 换元积分法 一、第一类换元法 二、第二类换元法

二、第二类换元法 第二节 一、第一类换元法 换元积分法 第四章

基本思路 设FC)口f(),u口口(x)可导，则有 dF[☐(x)]Cf[□(x)]▣x)dx 口(x1口(dx CF[口(x]OC口F()DCum(w 口(du u(x) 第一类换元法 口(x)]口Ox)dx (u)du 第二类换元法

第二类换元法 第一类换元法 基本思路 设 可导, 则有

一、第一类换元法 定理1，设f()有原函数，u口□(x)可导，则有换元 公式 I(x口xirC(wdu 口☐(x) 即 I口(x]口xdxC可(C(x)dD(x) (也称凑微分法

一、第一类换元法 定理1. 则有换元 公式 (也称 即 凑微分法)

注： 由定理可见，虽然OU(x)x)dx 是一整体记号，但可把dx视为自变量微分 pòf(x)乃x)=òfU(x)(x)一凑微分 òf(u)d:—换元 【F)+C]g一一回代 =F(x)]+C 步骤： 凑微分；换元求出积分；回代原变量

注: 由定理可见，虽然 是一整体记号，但可把 视为自变量微分 ——凑微分 步骤： 凑微分；换元求出积分；回代原变量 ——换元 ——回代

例1.求 解：m22r2x =2in2.d2x） .凑微分 含2心nd一-换元 w-c é1 cos(2x)+C. .回代原变量

例1. 求 解: -凑微分 -换元 -回代原变量

例2.求ax口b)"d (m▣□) 解：令u口ax☐b,则du口adx,故 原式=区”Ld上14。 a 注：当m口1时

例2. 求 解: 令 则 故 原式 = 注: 当 时

例3.求

例3. 求 解:

dx 例4.求 想到公式 du dx Ox ☐arctan u 令"则ddx 1-a arctan u☐C

例4. 求 解 : 令 则 想到公式

dx 例5.求 (a▣0) a2 x 解： dx 72☐x arcsin'☐C a du 想到 arcsinu☐C [口(x)I口CdxE(O(x)d☐(x) (直接凑微分

例5. 求 想到 解: (直接凑微分 )

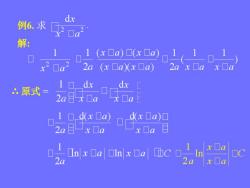
dx 例6.求 2 Oa" 解： 1(xa)☐(x☐a) x2a2 2a (x☐a)(x☐a) 原式 2胃 C,n*a OIn Cal Cc B,In 2a

例6. 求 解: ∴ 原式 =