《高等数学》课程教学资源（课件讲稿）第一章 函数与极限_1-5 极限运算法则

第五节 极限运算法则 一、无穷小运算法则 二、 极限的四则运算法则 三、复合函数的极限运算法则

二、 极限的四则运算法则 三、 复合函数的极限运算法则 一 、无穷小运算法则 第五节 极限运算法则

一、无穷小运算法则 定理1.有限个无穷小的和还是无穷小 证：考虑两个无穷小的和.设lim&=0,limB=0, x→x0 x→x0 Ve>0,381>0,当00,当0<x-x0<62时，有B< 取6=min{6,d2),则当0<x-xo<6时，有 a+Bsa+B<号+号=8 因此 lim(a+β)=0. x→x0 这说明当x→xo时，a+B为无穷小量

  min 1 ,  2 , 时, 有 一、 无穷小运算法则 定理1. 有限个无穷小的和还是无穷小 . 证: 考虑两个无穷小的和 . 设   0 , 当 时 , 有 当 时 , 有 取 则当     0 0 x x        2 2       因此 这说明当 时, 为无穷小量

类似可证：有限个无穷小之和仍为无穷小 说明：无限个无穷小之和不一定是无穷小 例如， 1.1 lim nn

说明: 无限个无穷小之和不一定是无穷小 ! 例如， 1 1 1 lim n  n n n           1 类似可证: 有限个无穷小之和仍为无穷小

定理2，有界函数与无穷小的乘积是无穷小 证：设Vx∈U(xo,d),u≤M 又设lima=0,即6>0,382>0，当x∈U(xo,82) x→X0 时，有a 取6=min{61,62},则当xeU(xo,6)时，就有 ua=ua≤M·&=& 故lim ua=0,即uc是x→xo时的无穷小 X→x0 推论1，常数与无穷小的乘积是无穷小 推论2，有限个无穷小的乘积是无穷小

定理2 . 有界函数与无穷小的乘积是无穷小 . 证: 设 u  M 又设 lim 0, 0    x x 即   0 , 当 时, 有 M    取 min , , 1 2     则当 ( , ) 0 x U x    时 , 就有 u  u       M M 故 即 是 时的无穷小 . 推论 1 . 常数与无穷小的乘积是无穷小 . 推论 2 . 有限个无穷小的乘积是无穷小

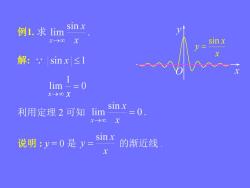
例1，求lim sinx x→00X sinx V= 解：sinx≤1 1im=0 X→0X sinx 利用定理2可知lim =0 x-→00 说明：y=0是y= sinx 的渐近线 x

例1. 求 解: 0 1 lim  x x 利用定理 2 可知 说明 : y = 0 是 的渐近线 . x x y sin 

二、极限的四则运算法则 定理3.若limf(x)=A,limg(x)=B,则有 lim[f(x)±g(x)]=limf(x)±limg(x)=A±B 证：因limf(x)=A,limg(x)=B,则有 f(x)=A+a,g(x)=B+阝 (其中a,B为无穷小) 于是 f(x)±g(x)=(A+a)±(B+B) =(A±B)+(a±B） 由定理1可知@±阝也是无穷小，再利用极限与无穷小 的关系定理，知定理结论成立

二、 极限的四则运算法则 lim f ( x)  A, lim g ( x)  B , 则有 证: 因 lim f ( x)  A, lim g ( x)  B , 则有 f ( x)  A   , g ( x)  B   (其中  ,  为无穷小) 于是 f ( x)  g ( x)  ( A   )  (B   )  (A  B)  (   ) 由定理 1 可知    也是无穷小, 再利用极限与无穷小 的关系定理 , 知定理结论成立 . 定理 3 . 若

推论：若limf(x)=A,limg(x)=B,且f(x)≥g(x) 则A≥B 提示：令p(x)=f(x)-g(x) 利用保号性定理证明 说明：定理3可推广到有限个函数相加、减的情形

推论: 若 lim f ( x)  A, lim g ( x)  B, 且 f ( x)  g ( x), 则 A B .  ( x)  f ( x)  g ( x) 利用保号性定理证明 . 说明: 定理 3 可推广到有限个函数相加、减的情形 . 提示: 令

定理4.若limf(x)=A,limg(x)=B,则有 lim[f(x)g(x)]=lim f(x)limg(x)=4B 提示：利用极限与无穷小关系定理及本节定理2证明 说明：定理4可推广到有限个函数相乘的情形 推论1.lim[Cf(x)]=Clim f(x) (C为常数) 推论2.lim[f(x)]”=[limf(x)]” (n为正整数) 例2.设n次多项式Pn(x)=a0+ax++anx”,试证 lim P (x)=Pn(o). x→x0 证：lim P.(x)=ao+a41limx++an1imx” x→X0 =P,(o)

定理 4 . 若 lim f ( x)  A, lim g ( x)  B , 则有 提示: 利用极限与无穷小关系定理及本节定理2 证明 . 说明: 定理 4 可推广到有限个函数相乘的情形 . 推论 1 . lim[C f ( x) ]  C lim f ( x) ( C 为常数 ) 推论 2 . n n lim[ f ( x) ]  [lim f ( x)] ( n 为正整数 ) 例2. 设 n 次多项式 试证 lim ( ) ( ). 0 0 P x P x n n x x   证:   lim ( ) 0 P x n x x

定理5.若1imf(x)=A,limg(x)=B,且B0,则有 limf() lim f(x)4 8(x) limg(x)B 例3. x3-1 1im(x3-1) lim- x→2 x→2X1 5x+3 lim(x2-5x+3) x-→2 (dlimx)3-1 x=2时分母不为0I x→2 (limx)-5limx+3 x→2 x→2 7 3

定理 5 . 若 lim f ( x)  A, lim g ( x)  B , 且 B≠0 , 则有 x = 2 时分母不为 0 ! 例3. 3 2 2 2 lim( 1) lim( 5 3) x x x x x       3 2 2 2 2 (lim ) 1 (lim ) 5lim 3 x x x x x x        7 . 3  

定理6.若1imxn=A,lim y=B,则有 n-→00 n→0 (l)lim(xm±yn)=A±B n-→00 (2) lim xnyn=AB n→oo (3) 当yn≠0且B≠0时，lim= A n-→oyn B 提示：因为数列是一种特殊的函数，故此定理可由 定理3,4,5直接得出结论

定理6 . 若 lim x A, lim y B , n n n n     则有 (1) lim ( ) n n n x  y  n n n x y  (2) lim (3) 当 y  0且 B  0时, n B A y x n n n   lim  A  B  AB 提示: 因为数列是一种特殊的函数 , 故此定理 可由 定理3 , 4 , 5 直接得出结论