《高等数学》课程教学资源（课件讲稿）第二章 导数与微分_2-3 高阶导数

第三节 高阶导数 一、高阶导数的概念 二、高阶导数的运算法则

二、高阶导数的运算法则 第三节 一、高阶导数的概念 高阶导数

一、高阶导数的概念 引例：变速直线运动s口s(t) 速度 即y☐s dt 加速度 a dt 即 a☐(s

一、高阶导数的概念 速度 即 加速度 即 引例：变速直线运动

定义.若函数y口f(x)的导数y中fx)可导，则称 了G的导数为/的二阶导数，记作或？.即 d x 类似地，二阶导数的导数称为三阶导数，依次类推， n☐1阶导数的导数称为n阶导数，分别记作 y四 或 d"y dx3 dx

定义. 若函数 的导数 可导, 或 即 或 类似地 , 二阶导数的导数称为三阶导数 , 阶导数的导数称为 n 阶导数 , 或 的导数为 的二阶导数 , 记作 依次类推 , 分别记作 则称

例1.设y口aa1x□a2x2D□anx”,求y例 解：y☐a1C2a2xC3a3x2C☐☐anx回 y0☐2la2C32a3xCD□n(nOl)anxm 依次类推，可得 ym☐nan 思考：设y口x(口为任意常数)，问ym口？ (x0)m）0C(001)(002)0(00nO1)xD

设 求 解: 依次类推 , 例1. 思考: 设 问 可得

例2.设y☐e,求y回 解：yaem,y四aeax,y吧a3e匹 ym☐a"eax y中 1x 特别有 (ex)(n) ☐ex y▣C 例3.设y☐n(1☐x),求ym □x)2 12 (1☐x)2, y☐（▣）2 1☐x)3 U,ywc(a（n (1口x)” 规定0！=1 思考：y□ln(1x),y,cDa (1☐x)

例2. 设 求 解: 特别有: 解: 规定 0 ! = 1 思考: 例3. 设 求

例4.设y☐sinx,求ym 解：y中cosx口sin(x口乏) ycos(x口)口sin(x口'D变) Dsin(x口2) ycos(x口2)口sin(x口3) 一 般地，(sinx)m☐sin(xCn) 类似可证： (cosx)m☐cos(xCn)

例4. 设 求 解: 一般地 , 类似可证:

例5.设f(x)□3x3口x2x,求使f(0)存在的最高 阶数n☐2 分析 ,x□0 2x3, x口0 2x3U0 口fq0)▣lim 0 x000 X f12x2,x☐0 4x3☐0 0f0x) f0)口lim 16x2, x□0 0 x009 又f0) Clim 6x20 0 24x,x☐0 x000 12x,x☐0 )E lim 12x2g0 口0 x009 但是f⑩)☐12，f⑩)□24，口f0)不存在

例5. 设 求使 存在的最高 分析 : 但是 不存在 . 2 又 阶数

二、高阶导数的运算法则 设函数u口u(x)及v口v(x)都有n阶导数，则 1.(u□y)m☐0m☐vm 2.(Cu)0m)☐Cm(C为常数) 3.( u2v☐ 规律 mn加(kDra, k! ☐0☐w0 莱布尼茨Leibniz)公式

规律 二、高阶导数的运算法则 都有 n 阶导数 , 则 (C为常数) 莱布尼茨(Leibniz) 公式 设函数 及 规律

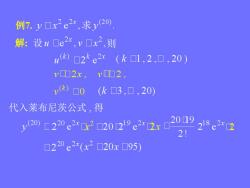
例7.y☐.x2e2r,求y20 解：设u☐e2x,v口x2,则 k)☐2ke2x(k☐1,2，☐，20) vD2x,v□2 ()0 (k☐3，▣，20 代入莱布尼茨公式，得 y20C220e2202021°e22x2019 18e22 21 口220e2r(x2☐20x☐95)

例7. 求 解: 设 则 代入莱布尼茨公式 , 得

内容小结 高阶导数的求法 (1)逐阶求导法 (2)利用归纳法 (3)间接法 利用已知的高阶导数公式 如下列公式 (sinx)() ☐sin(xCn) (cosx)) ☐cos(xLnξ) E()” n! a☐x (ax)"回 (4)利用莱布尼茨公式

内容小结 (1) 逐阶求导法 (2) 利用归纳法 (3) 间接法 —— 利用已知的高阶导数公式 (4) 利用莱布尼茨公式 高阶导数的求法 如下列公式