《高等数学》课程教学资源（课件讲稿）第一章 函数与极限_1-1 映射与函数

第一为 映射与画数 一、映射 二、函数

二、 函数 一 、映射 第一节 映射与函数

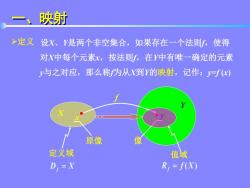
映射 >定义设X、Y是两个非空集合，如果存在一个法则f,使得 对X中每个元素x,按法则f,在Y中有唯一确定的元素 y与之对应，那么称为从X到的映射，记作：J=f) 原像 像 定义域 值域 Di=X R,=f(X)

一、映射 定义 设X、Y是两个非空集合，如果存在一个法则f，使得 对X中每个元素x，按法则f，在Y中有唯一确定的元素 y与之对应，那么称f为从X到Y的映射，记作：y=f (x) X Y x y f 原像 像 定义域 值域

●注 (1) 映射的三要素：定义域、值域的范围、对应法则； (2) 映射的像唯一，但原像不一定唯一； (3) 映射又称为算子，在不同数学分支中有不同的名称 X 非空集X X上的泛函 数集Y 非空集X X上的变换 非空集X 实数集X X上的函数 实数集Y

注 （1） 映射的三要素：定义域、值域的范围、对应法则； （2） 映射的像唯一，但原像不一定唯一； （3） 映射又称为算子，在不同数学分支中有不同的名称 非空集X 数集Y 非空集X X上的变换 非空集X 实数集X X上的函数 实数集Y f X上的泛函 X Y

逆映射 >满射、单射和双射 设f是从集合X到集合Y的映射

逆映射 设f是从集合X到集合Y的映射 满射、单射和双射 X Y f

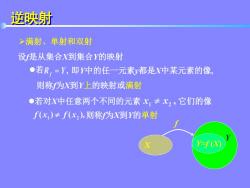
逆映射 >满射、单射和双射 设f是从集合X到集合Y的映射 ●若R,=Y,即Y中的任一元素y都是X中某元素的像， 则称f为到Y上的映射或满射 ●若对X中任意两个不同的元素X,≠x,它们的像 f(x)≠f(x,),则称f为X到Y的单射 Y=f(X)

逆映射 设f是从集合X到集合Y的映射 满射、单射和双射 若 即Y中的任一元素y都是X中某元素的像, 则称f为X到Y上的映射或满射 若对X中任意两个不同的元素 它们的像 则称f为X到Y的单射 X Y f Y=f (X)

逆映射 >满射、单射和双射 若f是从集合X到集合的映射 ●若R,=Y,即Y中的任一元素都是X中某元素的像， 则称f为到Y上的映射或满射 ●若对X中任意两个不同的元素x1≠x,它们的像 f(x)≠f(x,),则称f为X到Y的单射 ●若映射f既是满射又是单射， 则称f为一一映射或双射

逆映射 若f是从集合X到集合Y的映射 若映射 f 既是满射又是单射, 则称 f 为一一映射或双射. 满射、单射和双射 若 即Y中的任一元素y都是X中某元素的像, 则称f为X到Y上的映射或满射 若对X中任意两个不同的元素 它们的像 则称f为X到Y的单射 X Y f

逆映射 >满射、单射和双射 若f是从集合X到集合Y的映射 ●若R,=Y,即Y中的任一元素y都是X中某元素的像， 则称f为到Y上的映射或满射 ●若对X中任意两个不同的元素x1≠x2,它们的像 f(x)≠f(x,),则称f为X到Y的单射 ●若映射f既是满射又是单射： 则称f为一一映射或双射

逆映射 若f是从集合X到集合Y的映射 若映射 f 既是满射又是单射, 则称 f 为一一映射或双射. 满射、单射和双射 若 即Y中的任一元素y都是X中某元素的像, 则称f为X到Y上的映射或满射 若对X中任意两个不同的元素 它们的像 则称f为X到Y的单射 X f

>逆映射 若f是从到Y的单射，可定义一个从R,到X的新映射g g:R,→X,对每个yER,规定gy)=x,这x满足f(x)=y 这个映射g称为的逆映射，记作f ●注 (1)只有单射才存在逆映射 (②)逆映射f的定义域D,1=R 值域R1=X

逆映射 若f 是从X到Y的单射，可定义一个从 到X的新映射g 对每个 规定 这x满足 这个映射g称为f的逆映射，记作 注 (1) 只有单射才存在逆映射 (2) 逆映射 的定义域 值域

复合映射 >定义设有两个映射g:X→Y,f:Y,→Z,其中YcY 则由映射g和f可以定出一个从到Z的对应法则，它将每个 x∈X映成fg(x)eZ,这个对应法则确定了一个从到Z的 映射，这个映射称为映射和f构成的复合映射，记作f。g 即：fog:X→Z (fog)(x)=f[g(x)],xeX =g(9 ●注 sy=f(u) 8(x)】 (1)映射g和f构成复合映射的条件：R。cD (2)映射g和f的复合是有顺序的

复合映射 定义 设有两个映射 其中 则由映射g和f 可以定出一个从X到Z的对应法则，它将每个 映成 这个对应法则确定了一个从X到Z的 映射，这个映射称为映射g和f 构成的复合映射，记作 即： 注 (1) 映射g和f 构成复合映射的条件： (2) 映射g和f 的复合是有顺序的 Y1

>例题 ◆例1写出下列映射的定义域和值域，并回答如下问题： (1)映射f是否单射？是否满射？ (2)若存在逆映射，求出逆映射 1.设f:R→R,对每个x∈R,f(x)=x2 2.设映射f将平面上的一个圆心在原点单位圆周上的点 投影到x轴的区间-1,1上 /引 3. -1,1 对每个x引=咖：

例题 设 对每个 映射f 是否单射？是否满射？ 例1 设映射f 将平面上的一个圆心在原点单位圆周上的点 投影到x轴的区间 上 (1) 3. 写出下列映射的定义域和值域，并回答如下问题： (2) 若存在逆映射，求出逆映射 1. 2. 设 对每个