《高等数学》课程教学资源（课件讲稿）第五章 定积分_5-4 反常积分

第四节 第五章 反常积多 积分限有限 常义积分 被积函数有界 推 反常积分（广义积分）》 一、无穷限的反常积分 二、无界函数的反常积分

二、无界函数的反常积分 第四节 常义积分 积分限有限 被积函数有界 推广 一、无穷限的反常积分 反常积分 (广义积分) 反常积分 第五章

一、无穷限的反常积分 引例.曲线y口二 和直线x口1及x轴所围成的开口曲 边梯形的面积可记作 oo dx A回 其含义可理解为 b dx A▣lim 0 lim b00▣ 0 lim

一、无穷限的反常积分 引例. 曲线 和直线 及 x 轴所围成的开口曲 边梯形的面积 可记作 其含义可理解为

定义1.设f(x)口C[a,口口)，取b口a,若 lim (x)dx b00▣ 存在，则称此极限为(x)的无穷限反常积分，记作 f(x)dx口lim f(x)dx b▣口▣ 这时称反常积分f(x)dx收敛，如果上述极限不存在， 就称反常积分 f(x)dx发散 类似地，若f(x)口C(工，b],则定义 ()d lim()dx

定义1. 设 若 存在 , 则称此极限为 f (x) 的无穷限反常积分, 记作 这时称反常积分 收敛 ; 如果上述极限不存在, 就称反常积分 发散 . 类似地 , 若 则定义

若f(x)口C(工，口口)，则定义 ()dx Clim ()dxlim ()dx (c为任意取定的常数) 只要有一个极限不存在，就称 f(x)dr发散. 无穷限的反常积分也称为第一类反常积分 说明：上述定义中若出现山山山，并非不定型， 它表明该反常积分发散

则定义 ( c 为任意取定的常数 ) 只要有一个极限不存在 , 就称 发散 . 无穷限的反常积分也称为第一类反常积分. 说明: 上述定义中若出现 并非不定型 , 它表明该反常积分发散

若F(x)是f(x)的原函数，引入记号 F(D)▣limF(x):F(▣)▣limF(x) x0O▣ x0O□ 则有类似牛-莱公式的计算表达式： f(x)dF(x) oF(uF(a) f(x)dx·F(x) b OF(b)□F(I) f(wdF(x)

引入记号 则有类似牛 – 莱公式的计算表达式 :

00 dx 例1.计算反常积分 b10x2 00 d 0 解： [arctanx]m 1 1x 1x 思考： xdx 0对吗？ 分析： xdx 原积分发散！ 81x2 注意：对反常积分，只有在收敛的条件下才能使用 偶倍奇零”的性质，否则会出现错误

例1. 计算反常积分 解: 思考: 分析: 原积分发散 ! 注意: 对反常积分, 只有在收敛的条件下才能使用 “偶倍奇零” 的性质, 否则会出现错误

dx 例2.证明第一类p积分口 xP 当p>1时收敛；p1 时发散. 证：当p=1时有 a▣dx uu 当p≠1时有 ☐x p p1 10p ,1 10p 因此，当p>1时，反常积分收敛，其值为 p01 当p≤1时，反常积分发散

例2. 证明第一类 p 积分 证:当 p =1 时有 当 p ≠ 1 时有 当 p >1 时收敛 ; p≤1 时发散 . 因此, 当 p >1 时, 反常积分收敛 , 其值为 当 p≤1 时, 反常积分发散

例3.计算反常积分 dt(p) 解：原式口口ep 吧epdi p D e

例3. 计算反常积分 解:

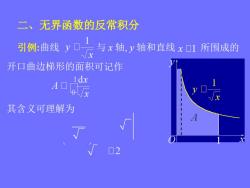
二、无界函数的反常积分 引例：曲线y0 与x轴，y轴和直线x□1所围成的 开口曲边梯形的面积可记作 1dx A 其含义可理解为 02

二、无界函数的反常积分 引例:曲线 与 x 轴, y 轴和直线 所围成的 开口曲边梯形的面积可记作 其含义可理解为

定义2.设f(x)口C(a,],而在点a的右邻域内无界 若极限 存在，则称此极限为函 数f(x)在[a,b]上的反常积分，记作 这时称反常积分 f(x)dx收敛，如果上述极限不存在， 就称反常积分 f(x)dx发散， 类似地，若f(x)口C[a,b),而在b的左邻域内无界， 则定义

定义2. 设 而在点 a 的右邻域内无界, 存在 , 这时称反常积分 收敛 ; 如果上述极限不存在, 就称反常积分 发散 . 类似地 , 若 而在 b 的左邻域内无界, 若极限 数 f (x) 在 [a , b] 上的反常积分, 则定义 则称此极限为函 记作