《高等数学》课程教学资源（课件讲稿）第十章 重积分_1001二重积分的概念与性质

重积分第十章第一节二重积分的概念与性质、二重积分的概念二、二重积分的性质三、对称定理08

第十章 重积分 第一节 二重积分的概念与性质

引言设函数f(x)在[a,bl上有界，在la,bl中任意插入若干个分点：a=x,<x, <x,<<x-1<x,=b,把区间[a,b]分成n个小区间[x,x,-],各小区间的长度依次为△x; =x,一x-,(i=1,2,…,n)。在每个小区间上任取一点 5, e[x,xi-i1,作乘积 f(5)Ax, ,并作出和 S=Zf(5)Ax, 记i-1几=max[△ri,Ar,,.…,△r,}，如果不论对[a,b]怎样划分，也不论在小区间[x1,x]上怎样选取点，只要当→0时，和S总趋于确定的极限I，那么称这个极限I为函数f(x)在区间[a,bl上的定积分，记为' f(x)dx = 1 =lim Z f(5,)Ax,入→01=100l08心个不不高数学教学部不不不

高等数学教学部 2

假定下面的各性质中列出的定积分都存在，且不考虑积分上下限的大小I' af (x) + Pg(x)ldx= α " f(x)dx+ βf" g(x)dxI'f(x)+ g(x)ldx-I' f(x)dx+J' g(x)dx.推论1[" kf(x)dx= kf' f(x)dx.推论2设a <c<b, 则f"f(x)dx= " f(x)dx+ T' f(x)dx2[, f(x)dx-I, f(x)dx =I" f(x)dx推论" f(x)dx- J" f(x)dx=f" f(x)dx001018个不不高教学教学部不不不

高等数学教学部 3  b a f (x)dx     b c c a f (x)dx f (x)dx.      b a c b c a f (x)dx f (x)dx f (x)dx      b a a c b c f (x)dx f (x)dx f (x)dx

dx= b-a.4 如果在区间[a,b]上,f(x)≥0, 则[f(x)dx ≥0, (a<b),推论1 如果在区间[a,b]上f(x)≤g(x),则 [" f(x)dx ≤f' g(x)dx, (a <b).推论 2I" f(x)dx≤ ["1 f(x) dx, (a<b).5设M及m分别是函数f(x)在区间[a,bl上的最大值及最小值，则m(b -a)≤f f(x)dx≤ M(b -a)6（定积分中值定理）如果函数f（x)在闭区间la,bl上连续，则在积分区间[a,bl 上至少存在一个点=, 使f(x)dx=f(E)(b-a)(a≤<b).00108中个不高教学教学部不不不

高等数学教学部 4

" f(x)dx称为函数 f(x)在区间 [a, b)积分学中值定理中，f()=-上的平均值当f(x)>0时，" f(x)dx在几何上表示由曲线 y=f(x)、直线 x=a、x=b及x轴所围成的曲边梯形的面积当f(x)<0时，["f(x)dx在几何上表示由曲线 y-f(x)、直线 x=a、x=L及x轴所围成的曲边梯形的面积的负值当,(x)有正有负时，[" f(x)dx在几何上表示由曲线 y-f(x)、直线 x=a、-b及x轴所围成的曲边梯形的面积的代数和对称定理① 若f(x)在[-a,al上连续且为偶函数，则f(x)dx=2f(x)dx②若f(x)在[-a,al上连续且为奇函数，则["f(x)dx=000108不不高尊教学教学部不不

高等数学教学部 5

二重积分的概念1、曲顶柱体的体积z= f(x,y)给定曲顶柱体：底：xoy 面上的闭区域D顶：连续曲面z=f(x,y)≥0侧面：以D的边界为准线，母线平行于 z 轴的柱面，求其体积。解法：类似定积分解决问题的思想（“分割，取近似求和，取极限”）eoo8个个个高等数学教学部

高等数学教学部 6 D z  f (x, y)

1）分割用一组曲线网将 D 任意分为 n个小区域△o,,α2,…·,△,分别以这些小区域的边界曲线为准线，作母线平行于z轴的柱面，这些柱面把原来的曲顶柱体分为n个小曲顶柱体.2）作近似当这些小区域的直径很小时，z = f(x,y)由于f(x,y)连续，对同一个小区域来说，f(x,J)变化很小，可将小曲顶柱体近似看做小f(5.n)平顶柱体于是，在每个小区域△α,中任取一D点(5i,n;), 则AV, ~ f(5i,n)A0;(5k,nk)(i = 1,2,...,n).001018个个个高等数学教学部不不个

高等数学教学部 7 D z  f (x, y) ( , ) i i f   ( , )  k  k (i  1,2,,n). i i i i V  f ( , )

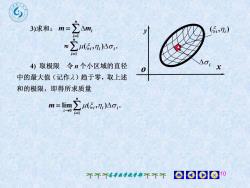
z = f(x,y)-EAV,~Zf(5i,n,)Ao,3)求和：V=f(5.,n.)4）取极限令n个小区域的直径中的最大值（记作）趋于零，取上述和的极限，即D得所求体积(Snk)Z f(si,n,)Ao.V = lim1-0i=l80008个不个高等数学教学部不不个

高等数学教学部 8 lim ( , ) . 1 0   n i i i i V f        n i V Vi 1  ( , ) . 1   n i i i i f    D z  f (x, y) ( , ) i i f   ( , )  k  k

62、平面薄片的质量设有一平面薄片，占有xov面上的闭区域D，在点(x,y)处的面密度为μ(x,y)，假定u(x,J)在D上连续且非负，试计算平面薄片的质量解法：类似定积分解决问题的思想（“分割，取近似，求和，取极限")(5i,n,)y1分割 用一组曲线网将 D 任意分为n个小区域Aoi,Ao.,..",Non.NoiX2）　作近似　当这些小区域的直0径很小时，由于uμ(x,y)连续，对同一个小区域来说，u(x,J)变化很小，可将μ(x,J)近似看成常数，于是，在每个小区域△,中任取一点(si,ni)，则Am, ~ μ(5i,n,)Ao, (i = 1,2,..,n).001018中个个个高等数学教学部不不不

高等数学教学部 9 mi   i i  i  ( , ) (i  1,2,,n).  i  ( , ) i i x y o

ZAm3)求和：m1(5i,n.)N-WVu(Ei,n;)Ag ;.i=1Noi4）取极限令n个小区域的直径X0中的最大值（记作几）趋于零，取上述和的极限，即得所求质量Em = limμ(i,n;)Ag,1-0i=10010个不不高等数学教学部不不不

高等数学教学部 10  i  ( , ) i i x y o ( , ) . 1   n i   i i  i   n i m mi 1  lim ( , ) . 1 0   n i m   i i  i  