《高等数学》课程教学资源（课件讲稿）第十一章 曲线积分与曲面积分_1102对坐标的曲线积分

第十一章曲线积分和曲面积分第二节对坐标的曲线积分对坐标的曲线积分的概念与性质二、对坐标的曲线积分的计算法三、两类曲线积分之间的联系0

第十一章 曲线积分和曲面积分 第二节 对坐标的曲线积分

+在定积分中，求质点受变力F=F(x)作用沿直线（x轴）从点A到点B所做的功，假定力F平行于x轴元素法选x为积分变量，[a,b为积分区间，取一小区间[x,x+dx]c[a,b]，功的元素为dW = F(x)dx,BXW =I' F(x)dx.所求功为 a x x+dxb设F是常力，质点受F作用沿直线从点A到点B，F对质点所做的功W = F.AB =IFI-IABIcosOHVBxO001018中个不个高数学教学部不不不

高等数学教学部 2 dW  F(x)dx, x     O a x b  x  dx A B ( ) .   b a W F x dx x    O A  F  B y

S、对坐标的曲线积分的概念与性质1、变力沿曲线所做的功y下求质点受变力BF(x,y)= P(x,y)i +Q(x,y)i 作用沿M.-M.Ayi平面曲线L从点A到点B所做的功LM,Ax(1)分割 在 L 上任意插入 n-1 个分M,M,点M,M,,...,M,,将L分成n 个小弧A段 M-M, (i=1,2,.,n),x0M。= A,M,=B，As,表示 Mi-iM,的长度同时也表示小弧段本身，并记M,(x,,y,),Ax, = x, - xi-1,Ay; = y; - yi-1oo8个不高等教学教学部不不不

高等数学教学部 3 o x y A B L Mn1 Mi Mi1 M2 M1 xi i y (i  1,2,,n), Mi1Mi Mi1Mi ( , ), , . i i i i  i  i1 i  i  i1 M x y x x x y y y

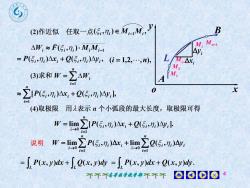
(2)作近似 任取一点(5,n;)eM-M, JBM, M.-AW, ~ F(5,,n,).M,M,-1Ay,L= P(5,,n,)Ax, +Q(5,n,)Ayi,(i = 1,2,..",n),M,AxM,M(3)求和 W-AW,Ai=lx0~Z[P(5,n,)Ax, +Q(5,n,)Ay,l,(4)取极限用表示n个小弧段的最大长度，取极限可得1E[P(5i,n;)Ax, + Q(5,n;)Ay ].W = lim10i=1≥ P(5,n)Ax, limZ(5,n,)4y,说明W - lim1→0120i=1-l-J, P(x, y)dx + , o(x, )dy = J, P(x, y)dx + Q(x, y)dy.00108个不高教学教学部不不不

高等数学教学部 4 ( , ) ,  i i  Mi1Mi 1 ( , )    Wi F  i i MiMi   ( , ) ( , ) , i i i i i i  P   x  Q   y (i  1,2,,n),   n i W Wi 1  [ ( , ) ( , ) ], 1    n i i i i i i i P   x Q   y o x y A B L Mn1 Mi Mi1 M2 M1 xi i y lim [ ( , ) ( , ) ]. 1 0    n i i i i i i i W P   x Q   y           n i i i i n i i i i W P x Q y 1 0 1 0 lim ( , ) lim ( , )  

S2、对坐标的曲线积分的概念和性质定义设 L 为xOy面内从点 A 到点 B 的一条有向光滑曲线弧，函数P(x,y),Q(x,J)在 L 上有界.在 L 上沿 L 的方向任意插入一点列M,(xi,J),M2(x2,y2),.",Mn-1(x,-1,yn-1),把L 分成 n 个有向小弧段,Mi--M, (i =1,2,...,n;M, = A,M, = B),记△x, =x,-x,-1，Ay; = y; -yi-1. 点(5i,n,)为 M-M,任意取定的点，作乙 P(5,n,)△x,. 如果当各小弧段乘积P(5;,n,)△x,(i =1,2,.,n),并作和i-1的长度的最大值入→0时，这和的极限总存在，则称此极限为P(x,y)在有Z P(5i,n,)Ax).向曲线弧 L 上对坐标x 的曲线积分,记为[ P(x,y)dx =limi-1001018个不不高教学教学部不不不

高等数学教学部 5 Mi1Mi Mi1Mi

S(5,n)Ay;存在，则称该极限为Q(x,y)在有向同理，若极限lim1i-1n Zo(5,n;)Ay,.曲线弧L上对坐标y 的曲线积分,记为[,Q(x,y)dy=lim i-1其中P(x,y),Q(x,)叫做被积函数，L叫做积分弧段以上积分称为第二类曲线积分可以证明，若P(x,j),Q(x,y)在有向光滑曲线弧 L 上连续，则[, P(x,y)dx,[, Q(x,y)dy存在, 且记J, P(x, y)dx + J,Q(x, y)dy = I, P(x, y)dx + Q(x, y)dy,也可记为「 F(x,J)-dr，其中 F(x,y)= P(x,y)i +Q(x,y)jdr =dxi+dyi，dr称为有向曲线弧元素由引例知, W =[F-dr=[ P(x,y)dx+Q(x,y)dy001018中个不高教学教学部不不不

高等数学教学部 6

S假定各性质中的曲线积分都存在性质 1（线性）设α,β是常数，则[, [aFi(x, y)+ βF,(x,y)] dr = αf,[F(x, y) dr + β], F,(x, y) dr推论(1)f, [F(x,y)+ F,(x, y)] dr= ,[Fi(x, y) dr + f, F,(x, y) dr ;(2)J, αFi(x, y) dr =αJ, F(x,y) · dr.性质 2（对区间的可加性）设有向曲线弧L由两段有向曲线弧L,和J, F(x,y) dr =J, F(x,y) dr + J, F(x,y) dr.L,组成，则性质 3（方向性）设有向曲线弧L，反方向有向曲线弧L，则[, F(x,y) dr =-J, F(x,y) dr.说明对坐标的曲线积分，特别要注意积分弧段的方向0010个不高等教学教学部不不

高等数学教学部 7

S定义和性质可以推广到积分弧段为空间有向曲线弧厂（总假定T光滑且具有有限长度）的情形[, P(x, y,z)dx = lim P(5,ni,5,)Ax;1→0ma[ Q(x, y,z)dy = lim1-1W[_R(x, y,z)dz = limR(5i,ni,5)Azi2-0i=1[ P(x,y,z)dx + I,Q(x, y,z)dy + [, R(x, y,z)dz= J P(x,y,z)dx + Q(x, y,z)dy + R(x, y,z)dz.[ A(x, y,z)·dr = P(x,y,z)dx+Q(x, y,z)dy+ R(x, y,z)dz.A(x, y,z)= P(x, y,z)i +Q(x, y,z)j + R(x, y,z)k, dr = dxi + dyj + dzk0008个不高教学教学部不不不

高等数学教学部 8 ( , , ) lim ( , , ) ; 1  0   n i dx P i i i xi P x y z       ( , , ) lim ( , , ) ; 1  0   n i i i i i Q x y z dy Q y      ( , , ) lim ( , , ) . 1  0   n i i i i i R x y z dz R z              P(x, y,z)dx Q(x, y,z)dy R(x, y,z)dz  P(x, y,z)dx  Q(x, y,z)dy  R(x, y,z)dz.     A x y z dr  ( , , ) A(x, y,z) P(x, y,z)i Q(x, y,z) j R(x, y,z)k,        dr dxi dyj dzk.         P(x, y,z)dx  Q(x, y,z)dy  R(x, y,z)dz. 

三、对坐标的曲线积分的计算法定理 1设函数P(x,y)、Q(x,y)在有向曲线弧 L 上连续，平面曲线x = (t)L 的参数方程为(α≤t≤β)，当参数t单调地由α变到β时,(y = y(t)相应的点M(x,y)从起点运动到终点，(t)、y(t)在[α,βI上具有一阶连续导数且p"(t)+y"(t)±0，则曲线积分[ P(x,y)dx+Q(x,y)dy存在,且 J, P(x, y)dx +Q(x, y)dy = f'(P[p(t),y(t)k'(t)+ Q[o(t),y(t)lv'(t)dt.说明积分下限α一定要对应于L的起点，而积分上限β一定要对应于L的终点，α不一定小于β证假定当参数t由α变到β时，L上的点M(xy)依点A至点B的方向描出曲线L，它们对应于一列单调增加的参数值α = to,ti,t2,..,tn-1,tn = β,Z由对坐标的曲线积分的定义知[ P(x,y)dx= limP(5.,n;)Ax;i=10008中不不高尊教学教学部不不

高等数学教学部 9 P(x, y)dx Q(x, y)dy {P[ (t), (t)] (t) L            Q[(t),(t)](t)}dt

设点(i,n;)对应的参数值为t,， 即E, =p(t,),n; =(t,),，ti-1 ≤t; ≤t;Ax, =x, -xi-I = p'(t)at, 其中at, = t, -t-l, ti- ≤t, ≤t,.: J, P(x, y)dx = lim Z P(5),n,)Ax, = lim E P[0(t,),y(t,)k0'(t)At,2-0i1- lim P[g(t,),y(t,)k'(t,)At, =[" P[o(t),y(t)lo'(t)dt,J,(x, y)dx =- I'e[p(t),y(t)ly'(t)dt,同理,/ P(x, y)dx +Q(x, y)dy = ['(P[p(t),y(t)l'(t) +Q[p(t),y(t)ly'(t)dt.这里，积分下限α对应于L的起点，积分上限β对应于L的终点00810个不不高教学教学部不不不

高等数学教学部 10 xi  xi  xi1 ( ) , i i     t      n i i i i L P x y dx P x 1 0 ( , ) lim ( , )  i i n i i i lim P[ ( ), ( )] ( )t 1 0              i i n i i i lim P[ ( ), ( )] ( )t 1 0             [ ( ), ( )] ( ) ,      P  t  t   dt ( , ) [ ( ), ( )] ( ) ,       Q x y dx Q  t  t   dt L P(x, y)dx Q(x, y)dy {P[ (t), (t)] (t) L             Q[(t),(t)](t)}dt