《高等数学》课程教学资源（课件讲稿）第十一章 曲线积分与曲面积分_1103格林公式及其应用

第七章曲线积分与曲面积分第三节格林公式及其应用格林公式福二、平面上曲线积分与路径无关的条件三、二元函数的全微分求积08

第七章 曲线积分与曲面积分 第三节 格林公式及其应用

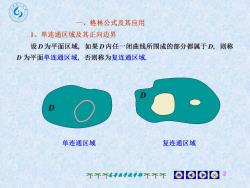
格林公式及其应用1、单连通区域及其正向边界设D为平面区域，如果D内任一闭曲线所围成的部分都属于D，则称D为平面单连通区域，否则称为复连通区域D单连通区域复连通区域001018个不不高等数学教学部不不不

高等数学教学部 2 D D

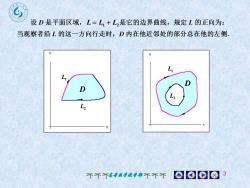
设D是平面区域，L=L,+L,是它的边界曲线，规定L的正向为当观察者沿L的这一方向行走时，D内在他近邻处的部分总在他的左侧D0018不不不高数学教学部不不不

高等数学教学部 3 L2 D L1 L2 L1 D

2、格林公式定理 1设闭区域D由分段光滑的曲线L围成,函数P(x,J)及Q(x,y)aQ ap在 D上具有一阶连续偏导数, 则有[,Pdx+Qdy= J()dxdy(1)ayaxn其中L是D的取正向的边界曲线公式(1)叫做格林公式，它表明了沿闭区域边界L的曲线积分可以通过平面闭区域D上的二重积分来表达apaQf, Pdx+ Qdy= J](分析　欲证)dxdyaxayDTrap只需证fPdx=-dxdyJDaya0福f.oly-JldxdyaxD001018个个高等数学教学部个不个

高等数学教学部 4        D L dxdy yP xQ Pdx Qdy ( )      D L dxdy yP Pdx     D L dxdy xQ Qdy

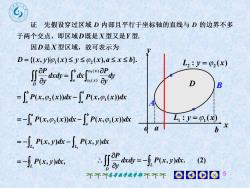
证先假设穿过区域D内部且平行于坐标轴的直线与D的边界不多于两个交点，即区域D既是X型又是Y型因D是X型区域，故可表示为D =((x,y)pi(x)≤y≤p,(x),a≤x≤b)L, : y = P,(x)Jo-agDB=I' P(x,P,(x)dx-I" P(x,pi(x)dxL : y= p(x)=-f P(x, P,(x)dx-' P(x,p(x)dxXb=-J, P(x,J)dx-J, P(x,y)dxJ% d-f x d(2)--f P(x,y)dx,ayD00108个不高等数学教学部不不不

高等数学教学部 5 y x o a b D : ( ) L1 y  1 x : ( ) L2 y  2 x A B dy y P dxdy dx y P x x b a D         ( ) ( ) 2 1       b a b a P(x,2 (x))dx P(x,1 (x))dx      2 1 ( , ) ( , ) L L P x y dx P x y dx ( , ) ,    L P x y dx ( , ) . (2)        L D dxdy P x y dx y P      b a a b P(x,2 (x))dx P(x,1 (x))dx {( , ) ( ) ( ), }. D  x y 1 x  y  2 x a  x  b

S因D是Y型区域，故可表示为VED= ((x,y)yi(y)≤x≤yz(y),c≤y≤d)dD1odab-ToraoL, : x=yi(y)-["Q(y,(y), y)dy - " Q(y.(y),y)dyL4 :x=V2(y)CCx- f' e(v,(y), y)dy + ,e(v,(y),y)dy-J, Q(x,y)dy+ J, Q(x,y)dy = fiQ(x,y)dy,-1/% - (s ).(3)2apf Pd+Qdy = J[()dxdy(2)+(3),知 ayaxD00108个不不高教学教学部不不不

高等数学教学部 6 {( , ) ( ) ( ), } D  x y  1 y  x  2 y c  y  d dx x Q dxdy dy x Q y y d c D         ( ) ( ) 2 1       d c d c Q( ( y), y)dy Q( ( y), y)dy  2  1     4 3 ( , ) ( , ) L L Q x y dy Q x y dy ( , ) ,   LQ x y dy y x o d : ( ) 4 2 L x  y D c C E : ( ) 3 1 L x  y ( , ) . (3)       L D dxdy Q x y dy x Q ( ) .          D L dxdy y P x Q Pdx Qdy     c d d c Q( ( y), y)dy Q( ( y), y)dy  2  1

如果区域D比较复杂，可引进辅助曲线，将D分成有限个部分区域，使得每个部分区域都是X型和Y型如果若区域D由按段光滑的闭曲线L,D,D,LB4C围成．如图，将D分成三个既是X型又是Y型的区域D,D,,D3DDf Pax+ Qdly ih+tPdx + QdyLLV-J, Pdx + Qdy + J, Pdx + Qdy + J, Pdx + QdyPdx + Qdy + f+ Pdx + Qdy + f.Pdx + QdyJL,+ACL+BA+CBapa0apapaQaQ小小小)dxdy +)dxdy +)dxdyaxayayaxaxayD2D3ap0)dxdy，这里，L,L,L,对 D 来说取正向.ayax0008个不不高教学教学部不不不

高等数学教学部 7 L L1 L2 L3 D D1 D2 D3        L L1 L2 L3 Pdx Qdy Pdx Qdy                      1 2 3 ( ) ( ) ( ) D D D dxdy y P x Q dxdy y P x Q dxdy y P x Q          L1 L2 L3 Pdx Qdy Pdx Qdy Pdx Qdy ( ) ,        D dxdy y P x Q A B C             L AC L BA L CB Pdx Qdy Pdx Qdy Pdx Qdy 1 2 3

如果区域D是复连通的，即区域D是由几条闭曲线所围成，可在D内引进一条或几条辅助曲线把D切割成单连通区域如图，引进辅助线AB，就把D切割V成单连通区域了Lf, Pdx+Qdy =(J+J,)Pdx+Qdy4-(aJ+JJ,)Pdx+QdyBDDaPyacly0小21ay-8og不不不高等数学教学部不不不

高等数学教学部 8 D L2 D L1 B A          2 1 ( ) BA L AB L Pdx Qdy      2 1 ( ) L L Pdx Qdy   L Pdx Qdy ( ) .        D dxdy y P x Q

aaS Pdx + Qdy = []说明ax(1)格林公式可记为aydxdyQPP(2)格林公式中，取Q=x,P=-y，则有 A=,f, xdy-ydx.(4)A=f xdy.类似地，取P = 0,Q= x，则有A=f (-y)dx.取P=-y,Q=0,则有0008个不个高数学教学部不不不

高等数学教学部 9 dxdy. P Q Pdx Qdy x y D L        . (4) 2 1    L A xdy ydx ( ) .    L A y dx .   L A xdy

2例1求星形线x3 +y2=a(α>0)所围区域的面积1x =acos' t,y = asin' t,t :0 →2元,a解北A-fi xdy- ydx1" [acos't.3asin'tcost -asin't.3acos' t(-sint)]dt号ncos'tsin'tdt -3n'.cos'tsin'tdt =6a'cos'tsin'td=6a (omn1-in a=-6aG -gm.例2证明：曲线积分（2ydx+3xdy的值为正向连续闭曲线L所围区域D的面积，L不经过原点、无重点、分段光滑，方向为逆时针方向aaT解 ↓, 2 ydx + 3xdy =(3x)(2 y)]dxdy= [ dxdy =(D 的面积),ayax000810个个高等教学教学部不个

高等数学教学部 10 cos , sin , : 0 2 , 3 3 x  a t y  a t t      L A xdy ydx 2 1    2 0 3 2 [ cos 3 sin cos 2 1 a t a t t asin t 3acos t( sint)]dt 3 2      2 0 2 2 2 cos sin 2 3 a t tdt    0 2 2 2 3a cos tsin tdt    2 0 2 2 4 6 (sin sin )  a t t dt ) 2 2 1 4 3 2 2 1 6 ( 2    a     . 8 3 2  a   L 2 ydx 3xdy        D y dxdy y x x [ (3 ) (2 )]   D dxdy x y o a D L a   2 0 2 2 2 6 cos sin  a t tdt