《高等数学》课程教学资源（课件讲稿）第九章 多元函数微分学_0901多元函数的基本概念

第九章多元函数微分法及其应用第一节多元函数的基本概念一、平面点集二、多元函数概念三、多元函数的极限四、多元函数的连续性08

第九章 多元函数微分法及其应用 第一节 多元函数的基本概念

平面点集1、平面点集平面点集(1)二元有序实数组(xJ)的全体，即R2=R×R=((x,y)[x,yER)表示坐标平面坐标平面上具有某种性质P的点的集合，称为平面点集，记作E =((x,y)I(x,y)具有性质 P)如C = ((x,y)|x2 + y?<r"}, C=(PIoPl<r).000不不不高等数学教学部不不不

高等数学教学部 2 C  {P | OP  r}

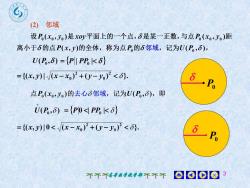
6(2)邻域设P(x,,y)是xoy平面上的一个点，S是某一正数，与点P(xo,y)距离小于S的点P(x,y)的全体，称为点P的S邻域，记为U(P,),U(P,8) = (Pl/PP, <8)=((x,y)/ /(x-x) +(y- yo) <8)SPo点P(x,yo)的去心S邻域，记为U(P,)，即U(P,) = (Pl0 </ PP, <8)=((x,y)l0 </(x-x,) +(y- yo) <8)SP0008个个个高数学教学部不不不

高等数学教学部 3 P0  ( , ) U P0   P | PP0 |   {( , )| ( ) ( ) }. 2 0 2  x y x  x0  y  y    ( , ) U P0    P 0 | PP0 |  {( , )| 0 ( ) ( ) }. 2 0 2  x y  x  x0  y  y   P0  

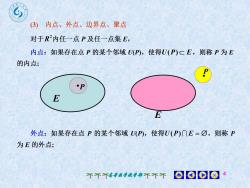
?内点、外点、边界点、聚点(3)对于R2内任一点P及任一点集E,内点：如果存在点P的某个邻域U(P)，使得U(P)CE，则称P为E的内点；EE外点：如果存在点P的某个邻域 U(P)，使得U(P)OE=O，则称P为E的外点；001018个个个高等数学教学部个不个

高等数学教学部 4 E P E P 

?边界点：如果点P的任一邻域内既含有属于E的点，又含有不属于E的点，则称P为 E的边界点'P边界：E的边界点的全体称为E的边界E记作E.说明 E的内点属于 E，外点不属于E,边界点可能属于E聚点：如果对于任意给定的S>0，点P的去心邻域U(P,S)内总有E中的点，则称P是E的聚点说明E 的聚点可能属于 E，也可能不属于E;E的内点是聚点，外点不是聚点，边界点可能是聚点008个不个高等数学教学部不不个

高等数学教学部 5 E P

业）区域(4)开集：如果点集E的点都是E的内点，则称E为开集闭集：如果点集E的边界EE，则称E为闭集连通集：如果点集E内任何两点，均可用一条包含于E的折线联接起来，则称E为连通集区域（或开区域）：连通的开集称为区域或开区域闭区域：开区域连同它的边界一起所构成的点集称为闭区域008个个个高等数学教学部

高等数学教学部 6

YX开区域(x,y)[1<x2 +2 <4)闭区域((x,y)[1≤x2+y2≤4)有界集：对于平面点集 E，如果存在某一正数 r，使得E C U(O,r),其中O为坐标原点，则称E为有界集无界集：一个集合如果不是有界集，则称为无界集0008个不不高等数学教学部不不不

高等数学教学部 7 x y o x y o

福二、多元函数概念定义1 设D 是R2的一个非空子集，称映射f:D→R为定义在 D 上的二元函数，通常记为z=f(x,y),(x,J)E D或z= f(P),PE D,其中点集D称为该函数的定义域，x、y为自变量，z为因变量函数的值域记为f(D)={z/ z= f(x,y),(x,J)e D)类似地定义三元及三元以上函数，二元及二元以上的函数称为多元函数.z = f(x,y),(x,y)e Dz= f(P),PED;u= f(x, y,z),(x,y,z)eQu= f(M),M e2;u= f(P),PeDu = f(x,X2,**.,xn),(xj,X2,*,x,)e D10008个不不高教学教学部不不不

高等数学教学部 8 z  f (x, y),(x, y) D z  f (P),P  D; u  f (x, y,z),(x, y,z) u  f (M),M ; u  f (x1 , x2 ,, xn ),(x1 , x2 ,, xn ) D u  f (P),P  D

arcsin(3-x2 - y2)例 1 求函数,f(x,y)=a的定义域Vx-y?1 J[3-x2 -y≤1 [2≤x2+y2≤4解一[x-y’ >0[x>y?x:. D=((x, y)/2≤x2 + y2 ≤4, x> y2)o08不不不高数学教学部不不个

高等数学教学部 9          0 3 1 2 2 2 x y x y         2 2 2 2 4 x y x y {( , )| 2 4, }. 2 2 2  D  x y  x  y  x  y

设函数z= f(x,y)的定义域为D，对于任意取定的P(x,y)E D，对应的函数值为z=f(x,y)，这样，以x为横坐标、y为纵坐标、z为竖坐标在空间就确定一点M(x,J,z)，当(x,y)取遍D上一切点时，得一个空间点集((x,J,z)I z=f(x,J),(x,y)e D)，这个点集称为二元函数的图形二元函数的图形通常是一张空间曲面z=f(x,y)00810不不不高尊数学教学部不不不

高等数学教学部 10