《高等数学》课程教学资源（课件讲稿）第九章 多元函数微分学_0904多元复合函数的求导法则

第九章多元函数微分法及其应用第四节多元复合函数的求导法则0

第九章 多元函数微分法及其应用 第四节 多元复合函数的求导法则

一元函数与多元函数复合的情形如果u=g(x)在点x 可导，而y= f(u)在点u=g(x)可导，则复合函数y=fIg(x))在点x可导，且dydydy du或f'(u)·g'(x)dxdxdu dx定理1若函数u=@(t),v=(t)在点t可导，函数z=f(u,v)在对应点(u,μ)具有连续偏导数，则复合函数z=flβ(t), (t)I在点 t 可导，且有dzOz duOz dvdt Ou dt Ov dt0008中个不不高教学教学部不不不

高等数学教学部 2 f (u) g (x) dx dy     . dx du du dy dx dy 或  

定理1 若函数u=(t),v=(t)在点 t 可导，函数z=f(u,)在对应点(u,)具有连续偏导数，则复合函数z= flβ(t), (t))在点 t 可导，且有dz du Oz dydt ou dt Ow dt证设t取增量△t，则u、相应有增量△u,△v,z相应有增量△z.因z= f(u,v)在点(u,)处具有连续偏导数，则z= f(u,v)可微Ozaz由微分定义知，△zAu+△v+o(p) , (p = (u)2 +(△v)2)avQuAzOz AuOz Avo(p).. limlimav AtAtAt-0 △tt→0 Ou NtOz AuOzAvo(p)= limOu NtOv △tAt-→0pOz du.oz dv1Ov dtOu dt001018个不高等教学教学部不不不

高等数学教学部 3 z u v t t z t    0 lim   ) ( ) lim( 0 t o t v v z t u u z t                ] | | ( ) ( ) ( ) lim[ 2 2 0 t t t v t o u t v v z t u u z t                         . dt dv v z dt du u z        

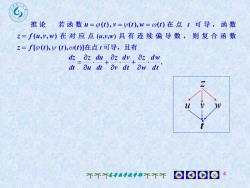
推论若函数u=(t),v=y(t),w=の(t)在点 t 可导，函数z=f(u,v,w)在对应点(u,v,w)具有连续偏导数，则复合函数z=flp(t),y (t),の(t)在点t可导，且有dz Oz duOz dv Oz dwdt Ou dt Oy dt aw dt0008个不个高尊数学教学部不不不

高等数学教学部 4 z u v w t

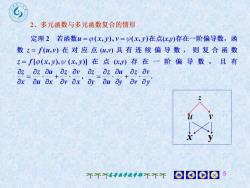
2、多元函数与多元函数复合的情形定理2 若函数u=β(x,),V=y(x,y)在点(x,)存在一阶偏导数，函数z=f(u,v)在对应点(u,")具有连续偏导数，则复合函数z=flp(x,y),y(x,y)) 在点 (x) 存在 一阶 偏 导数，且有Ozz OuOz Ovzz OuOz Ovax au ax v ax' ay Qu ay av ay000?不不不高尊数学教学部不不不

高等数学教学部 5 z u v x y

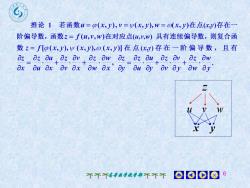
推论 1 若函数u=β(x,y),v=y(x,y),w=の(x,y)在点(xy)存在-阶偏导数，函数z= f(u,,w)在对应点(u,v,w）具有连续偏导数，则复合函数z=f[p(x,j),y (x,y),の (x,y)l在点(xy)存在一阶偏导数，且有Oz Oz OuOz OvOz OwOzz Ouaz Ov.Oz Owax Qu axOv axOw ax' ay Ou ay Ov ayOw ayY10010不不不高尊数学教学部不不不

高等数学教学部 6 z u v w x y

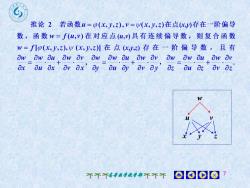
推论 2 若函数u=β(x,y,z),v=y(x,y,z)在点(xy)存在一阶偏导数，函数w= f(u,)在对应点(u,)具有连续偏导数，则复合函数w=flp(x,y,z),y(x,y,z)在点(xyz)存在一阶偏导数，且有Owaw OuawoyOwow duawaowowouwOyaxQu axOv axayQu ayv ayOz Qu OzOv Qz010不不不高尊数学教学部不不不

高等数学教学部 7 w u v x y z

3、其他情形定理3 若函数u=β(x,)在点(x,y)存在一阶偏导数，=(y)在点 可导，函数z=f(u,v)在对应点(u,)具有连续偏导数，则复合函数z=flp(x,y),y(y))在点(x,y)存在一阶偏导数，且有OzOz uOzz OuOz dvax Ou ax'ayau ayv dy80008不不不高等数学教学部不不不

高等数学教学部 8 z u v x y

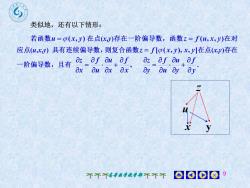
类似地，还有以下情形：若函数u=β(x,)在点(xy)存在一阶偏导数，函数z= f(u,x,y)在对应点(u,x,）具有连续偏导数，则复合函数z=f[p(x,y),x,在点(xj)存在azaf uafoz ?f ouof一阶偏导数，且有axOu Ox ax'dy Qu dydyoog不不不高数学教学部不不不

高等数学教学部 9 z x y u

Oz Oz例 设z=e" sinv,u=xy,v=x+y,求ox'ayOzuOz Ov解-e"sinv·y +e" cosyOx u ox :Ov Ox2= e*y[y · sin(x + y)+ cos(x + y)],Oz OuazazOv=e" sinv ·x +e" cosvQu Qyayav ay= e*y[x · sin(x + y)+ cos(x+ y)]00810个不不高教学教学部不不不

高等数学教学部 10 x z   e v u  sin e [ y sin(x y) cos(x y)], x y      y z   e [x sin(x y) cos(x y)]. x y      e v u  sin x u u z       x v v z       e v u  cos y u u z       y v v z       e v u  cos  y  x