《高等数学》课程教学资源（课件讲稿）第八章 向量代数与空间解析几何_0801向量及其线性运算

第八章向量与空间解析几何第一节向量及其线性运算向量的概念向量的线性运算N三、空间直角坐标系四、利用坐标作向量的线性运算五、向量的模、方向角、投影08

第八章 向量与空间解析几何 第一节 向量及其线性运算 一、向量的概念 二、向量的线性运算 三、空间直角坐标系 四、利用坐标作向量的线性运算 五、向量的模、方向角、投影

一、向量的概念向量：既有大小又有方向的量；B向量的表示：a或AB：自由向量：不考虑起点位置的向量：向量的相等：大小相等、方向相同的向量：向量的模（大小)：「a|或|ABl：单位向量：模为1的向量，é；零向量：模为0的向量，0，方向任意；00中个不不高等数学教学部不不不

高等数学教学部 2 A B  

将向量、b的起点重合，在两向量的所在平面上，若一个向量逆时针方向转过角度0后可与另一个向量的正向重合，则称0为向量a、b的夹角，记作(a,b)，θ=(a,b)=(b,a) (0≤0≤元).说明夫规定零向量和另一个向量的夹角可以是（0≤0≤元之间的任意一个角.已知两向量a、b，如果它们的夹角θ=0或θ=元，则称两向量平行记为a/b，两向量指向同向时θ=0，两向量指向反向时0=元元已知两向量a、b，如果它们的夹角θ=则称两向量垂直，记为2a工b，规定零向量指与任何向量都平行，也与任何向量都垂直两向量起点放在一起时，如果它们的终点和起点在同一直线上，则称两向量共线k(k≥3)个向量起点放在一起时，如果它们的终点和起点在同一平面内，则称这k个向量共面0010个不个高尊数学教学部不不

高等数学教学部 3

?二、向量的线性运算1、向量的加减法平行四边形法则：以同起点向量a、b为平行四边形相邻两边，以向量a的起点为起点的其对角线表示的向量为两个向量的和，记为a+bc=a+bCa+hbaABa三角形法则：设有两个向量a、b，任取一点A作AB=a，以B为起点作BC=b，连接AC，那么向量AC=c为两个向量a、b的和，记为a+b，即c=a+b.运算律：（1）交换律 a+b=b+a(2)结合律(a+b)+c=a+(b+c)00l08个不不高教学教学部不不不

高等数学教学部 4 a  b  a b    c a b      a  b  A B C

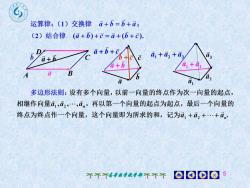
运算律：（1） 交换律 a+b=b+a;(2) 结合律(a+b)+c=a+(b+c)a+b+cDa, +a, +aai3a+ha, +azBaA多边形法则：设有多个向量，以前一向量的终点作为次一向量的起点，相继作向量a,a,，,a，，再以第一个向量的起点为起点，最后一个向量的终点为终点作一个向量，这个向量即为所求的和，记为a,+a，+··+a,0008个不不高数学教学部不不不

高等数学教学部 5 a  b  a b    A B C D a  b  a b    c  b c    a b c      1 a  a1 a2    a1 a2 a3      2 a  3 a 

设a为一向量，与a的模相同两方向相反的向量，叫做a的负向量记为-a.说明规定: a-b=a+(-b); a-a=a+(-a)=0.以同起点向量b的终点为起点、的终点为终点的对角线表示的向量为两个向量的差，记为a一b0a说明 |a+b[<[a|+|b|或|a-b<[a|+|b],Dba+h等号在两向量同号或反向时成立BfCA0008个个个高等数学教学部

高等数学教学部 6 a b    a  b  a  b  a b    A B C D

2、向量与数的乘法向量的数乘(a)设为常数，与向量a的乘积规定为：(1)a--a];（2）>0时，a与a同向；<0时，a与a反向：=0时，a=0说明1a=a; (-1)a=-a运算律：（1）交换律 ·a=a·;(2）结合律（μu)a= a(ua);（3）分配律 (a+ μu)a = Ma + ua;(a+ b)= a+ ab;向量的加法及数乘运算称为向量的线性运算008个个个高数学教学部不不个

高等数学教学部 7

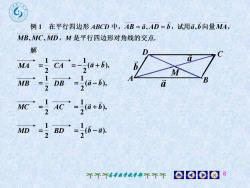
例1 在平行四边形ABCD中，AB=a,AD=b，试用a,b向量MAMB,MC，MD，M是平行四边形对角线的交点解D福aI(a+b),bMACA21MAB(a-b)DBaMB12AC -,(a+b)1-2MCBD(6-a),MD280008不不不高尊数学教学部不不个

高等数学教学部 8 MA 2 1  A B D C M a  b  a  CA ( ), 2 1 a b      MB 2 1  DB ( ), 2 1 a b     MC 2 1  AC ( ), 2 1 a b     MD 2 1  BD ( ). 2 1 b a    

向量的单位化(b)设e,表示与非零向量a同向的单位向量，则é，a=aé定理 1设向量a≠0，则向量b //a的充分必要条件是存在唯一的实数几，使b = Λa.证充分性假定b=aa，当>0时，b与a同向；当元=0时，b=0；当几<0时，b与a反向，均有b lla.必要性假定bllab取[[b与a同向时a取正，b与a反向时几取负，可知b=aa，a16al-|b].因为b与a同向；a=aa唯一性 假定b=a,b = ua =(-u)a=0 → =μ.0008中个不高教学教学部不不不

高等数学教学部 9  (  )a  0       

?点在轴上的坐标(c)给定一个点、一个方向及长度单位，则确定了一条数轴1家x对于数轴上一点 P，OPl/i，存在唯一实数x,oiP使oP=xi, p oP=xi x,实数x叫做轴上有向线段OP的值，定义为轴上点P的坐标轴上点P的坐标为x的充分必要条件是OP=xi010个不个高等数学教学部不不个

高等数学教学部 10 O   i P 1 x