《高等数学》课程教学资源（课件讲稿）第九章 多元函数微分学_0902偏导数

第九章多元函数微分法及其应用第二节偏导数偏导数的定义及其计算法二、高阶偏导数0

第九章 多元函数微分法及其应用 第二节 偏导数

偏导数的定义及其计算法1、偏导数的定义引言设函数y=f(x)在点x,的某个邻域内有定义．当自变量x在x处取得增量△x(点x+△r仍在该邻域内），相应地函数取得增量Ay=f(x。+△x)-f(x,).如果△x→0时△y与△x之比的极限存在，则称之为函数y=f(x)在x处的导数，并称y=f(x)在x,处可导f(x, +Ax)- f(x.)Aylimf'(x)= limArAx-0AxAx-→00008不不不高数学教学部不不不

高等数学教学部 2 . ( ) ( ) ( ) lim lim 0 0 0 0 0 x f x x f x x y f x x x             

S定义设函数z=f(x,J)在点(xo,y)的某一邻域内有定义，当y固定在y而x在x处有增量△x时，相应地函数有增量f(x, + Ax,yo)- f(xo,yo)存在,f(x, + Ar,yo)- f(x,y.), 如果 lim ArAr->0则称此极限为函数z=f(x,y)在点(xo,J)处对x的偏导数，记为azafzxx=x,或f(xo,Jo)Ox x=xoax x=xoV=VO=Joy=yo同理定义函数z=f(x,y)在点(xo,y)处对y的偏导数，为azaff(xo,Jo +Ay)- f(xo,yo)，记为lim, x=x或f,(xo,y)ayayAyAy->0x=XoX=X=yoy=yoy=yo008个个个高等数学教学部不不不

高等数学教学部 3

S如果函数z= f(x,y)在区域D内任一点(x,y)处对x的偏导数都存在，那么这个偏导数就是x、y的函数，它就称为函数z=f(x,y)对自变azaf 量x的偏导函数，记作z,或f (x,y)axaxafOz同理可以定义函数z=f(x,y)对自变量y的偏导函数，记作ayayz,或f,(x,y)说明求函数z=f(x,y)的偏导数，可采用一元函数的求导法.即对某一个自变量求偏导时，把其余变量看成常数偏导数的概念可以推广到二元以上的函数如三元函数u= f(x,y,z)在点(x,y,z)处对x的偏导数定义为f.(x,y,z)= lim (x+ Ax, ,z)- I(x, ,z)ArAr-→0001018个不不高教学教学部不不不

高等数学教学部 4 . ( , , ) ( , , ) ( , , ) lim0 x f x x y z f x y z f x y z x x       

例 1 求 z= x2 +3xy+ y2在点(1,2)处的偏导数。azOz = 3x+2y.解2x+3y;ayaxOzaz3×1+2×2=7"= 2×1+3×2=8,ax=2xoz 1 oz例2 设z=x(x>0,x±1)，求证：= 23.y axIn x ayOz证αzyxJ-1x'Inx,axayxoz1 ozXJJ-x'Inx =x+x* =2z.yaxIn x dyVInx008个个个高等数学教学部个不个

高等数学教学部 5    x z 2x  3y ;    y z 3x  2y .       2 1 y x x z 21 3 2  8 ,      2 1 y x y z 31 2 2  7 .    x z , y1 yx    y z x ln x, y y z x x z y x      ln 1 x x x yx y x y y ln ln 1 1    y y  x  x  2z

drdrdr例3 设r=2＋2+z2，证明：-1axayOz1ar解2xax2/x2+zOrary7)2 +(0)2 =1同理ay27OzAdu“是一个整体记号，不能拆分；说明1° 偏导数ax20求分界点、不连续点处的偏导数要用定义求008个个个高等数学教学部不不个

高等数学教学部 6 x r   x x y z 2 2 1 2 2 2     , r x  , r y y r    , r z z r    ( ) ( ) ( ) 1. 2 2 2           z r y r x r

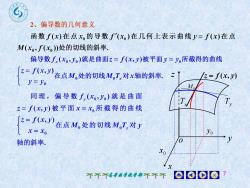
?2、偏导数的几何意义函数f(x)在点x.的导数f(x)在几何上表示曲线y= f(x)在点M(xf(x,))处的切线的斜率偏导数f(x,y)就是曲面z=f(x,y)被平面y=y,所截得的曲线[z= f(x,y)Z/z= f(x,y)在点M,处的切线M,T,对x轴的斜率.y=yoM同理，偏导数f(xo,yo)就是曲面Tz=f(x,y)被平面x=x.所截得的曲线[z= f(x,y)在点M.处的切线M.T,对yx = xo0轴的斜率XoX0008个不不高出学教学部不不不

高等数学教学部 7 y x z 0 x Ty o Tx 0 y M0 z  f (x, y)

?xyx2 + y2 +0例 4 讨论函数f(x,J)=x2+y在(0,0)点处的偏导x?+ y2 = 00数0-0f (0 + △x,0) - f (0,0)解=0,f.(0,0) = lim= limAxAr-→>0ArAx-→00-0f (0 + Ay,0) - f (0,0)f,(0,0) = lim= 0.lim同理AyAy-0AyAy-→0说明由例 4 知，函数z= f(x,y)的一阶偏导数存在，并不保证函数z=f(x,)的连续性，反之亦然连续一阶偏导数存在eolo8个不不高教学教学部不不不

高等数学教学部 8 (0,0) x f x f x f x    (0 ,0) (0,0) lim 0     x x 0 0 lim 0     0, (0,0) y f  0. y f y f y    (0 ,0) (0,0) lim 0     y y 0 0 lim 0   

新二、高阶偏导数设z=f(x,J)在域 D 内存在连续的偏导数：0z = f.(x,y),az= f,(x,y)ayax若这两个偏导数仍存在偏导数，则称它们是z=f（x，y）的二阶偏导数.按求导顺序不同，有下列四个二阶偏导数：0 oza'zaOzaz= fxy(x,y);= fxx(x,y);axay axaxoyaxax?aa"za'za(OzOz= f,x(x,y);= fy(x,y).axayayayaxOy2ay0008中不不不高等数学教学部不不不

高等数学教学部 9 ( , ) , f (x, y) y z f x y x z x  y      ( ) x z   ( ) y z x     ( ) x z y     ( ) ( , ). 2 2 f x y y z y z y  y y        2 2 x z    f (x, y);  x x x y z     2 f (x, y);  x y ( , ); 2 f x y y x z  y x     x 

a'z a'z a'z a'za'z例 5 设z = x~y2-3xy3- xy +1, 求ax?'Qyax'axay'ay2'Qx3OzOz解= 3x'y? -3y3 - y,= 2xy3 - 9xy2 - x,axay0'2 =6x'y-9y*-1,"za"z= 6xy2=6x2y- 9y2-1, axoyax?ayaxa'za'z=6y2- 2x3 -18xy,ax3ay定理如果函数 z=f(x,y)的两个二阶混合偏导数 fr,(xy)、f(xy)在区域 D 内连续，那么在该区域内有 fx,(xy)=fu(xy)说明本定理对n元函数的高阶混合导数也成立高阶混合导数在连续的条件下与求导次序无关000810个不高等教学教学部不不不

高等数学教学部 10 3 3 , 2 2 3 x y y y x z      2 9 , 3 2 xy xy x y z      6 , 2 2 2 xy x z    6 9 1, 2 2 2       x y y y x z 6 9 1, 2 2 2       x y y x y z 2 18 , 3 2 2 x xy y z     6 . 2 3 3 y x z   