《高等数学》课程教学资源（课件讲稿）第十一章_11-3格林公式

第三节格林公式及其应用格林公式二、平面上曲线积分与路径无关的条件三、二元函数的全微分求积四、小结练习题

第三节 格林公式及其应用 • 一、格林公式 • 二、平面上曲线积分与路径无关的条件 • 三、二元函数的全微分求积 • 四、小结 练习题

一、格林公式1、区域连通性的分类设D为平面区域，如果D内任一闭曲线所围成的部分都属于D，则称D为平面单连通区域，否则称为复连通区域D单连通区域复连通区域

一、格林公式 设D为平面区域, 如果D内任一闭曲线所围成 的部分都属于D, 则称D为平面单连通区域, 否 则称为复连通区域. 单连通区域 复连通区域 D D 1、区域连通性的分类

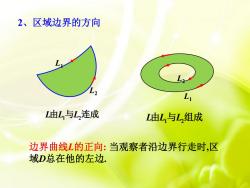
2、区域边界的方向LL由L,与L,连成L由L,与L,组成边界曲线L的正向：当观察者沿边界行走时，区2域D总在他的左边

边界曲线L的正向: 当观察者沿边界行走时,区 域D总在他的左边. 2、区域边界的方向 L L L 由 1 2 与 组成 L2 L1 L L L 由 1 2 与 连成 L2 L1

3、格林公式定理设闭区域D由分段光滑的曲线L围成函数P(x,y)及Q(x,y)在D上具有一阶连续的偏导数，则有apaQ)dxdy = Φ, Pdx + Qdy(1)axayD其中L是D的取正向的边界曲线公式（1）叫作格林公式注意：（1）P、Q在闭区域D上一阶偏导数的连续性;(2）曲线L是封闭的，并且取正向

3、格林公式 ( , ) ( , ) ( ) (1) . L D D L P x y Q x y D Q P dxdy Pdx Qdy x y L D   − = +     设闭区域 由分段光滑的曲线 围成， 函数 及 在 上具有一阶连续的 偏导数，则有 其中 是 的取正向的边界曲线 公式(1)叫作 定理 格林公式. 注意：(1) P、Q在闭区域D上一阶偏导数的连续性; (2) 曲线L是封闭的,并且取正向

证明(1)y=p,(x)RdD设区域D既是X-型又是Bx=(y)Y-型,即平行于坐标轴的x=V2(y)直线和L至多交于两点CC y=q(x)0d6D=((x,y)g(x)≤y≤p2(x),a≤x≤b)D=((x,y)yi(y)≤x≤2(y),c≤y≤d)

1 2 D x y x y x a x b =     {( , ) ( ) ( ), }   证明(1) 1 2 D x y y x y c y d =     {( , ) ( ) ( ), }   y o x a b cd 1 y x =  ( ) 2 y x =  ( ) D A B C E 2 x y = ( ) 1 设区域D既是X -型又是 x y = ( ) Y - 型 ,即平行于坐标轴的 直线和 L至多交于两点

rv() 0%dxdy = [" dy]dxaxJyi(y) axD-f" 2(y,(), y)dy-f" 2(y(y), y)dyQ(x, y)dy - (cur Q(x, y)dyECBEd(yx=yBQ(x, y)dy+ (rcAQ(x, y)dyCBEEACx=V(y)C=f, Q(x,y)dy*x0ap-7dxdy = Φ, P(x, y)dx同理可证ayD

D Q dxdy x   2 1 ( ( ), ) ( ( ), ) d d c c = − Q y y dy Q y y dy     ( , ) ( , ) CBE CAE = − Q x y dy Q x y dy   ( , ) ( , ) CBE EAC = + Q x y dy Q x y dy   ( , ) L = Q x y dy  同理可证 ( , ) L D P dxdy P x y dx y  − =    y x od 2 x y = ( ) D c CE 1 x y = ( ) B A 2 1 ( ) ( ) d y c y Q dy dx x   =   

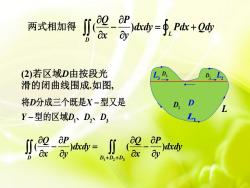
apaQM)dxdy = Φ, Pdx + Qdy两式相加得axayD(2)若区域D由按段光DLD,滑的闭曲线围成.如图将D分成三个既是X-型又是DD,LLY-型的区域D、D,、D,apapaQaQM)dxdy=)dxdyaxayayaxDD,+D2+D3

L D (2)若区域D由按段光 滑的闭曲线围成.如图, L1 L3 L2 D1 D2 D3 两式相加得 ( ) L D Q P dxdy Pdx Qdy x y   − = +     1 2 3 ( ) ( ) D D D D Q P Q P dxdy dxdy x y x y + +     − = −       1 2 3 D X Y D D D − − 将 分成三个既是 型又是 型的区域 、

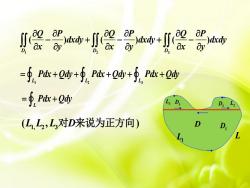
apapap0QaQaQJsJ)dxdy)dxdy)dxdy ++axaxayayaxayD3D,e Pdx+ Qdy+$, Pdx+Qdy+ Φ, Pdx+QdyJLJLs= $, Pdx + QdyL3DsD2(L,L,L,对D来说为正方向)DDL4

1 2 3 ( ) ( ) ( ) D D D Q P Q P Q P dxdy dxdy dxdy x y x y x y       − + − + −          L L L 1 2 3 = + + + + + Pdx Qdy Pdx Qdy Pdx Qdy    L = + Pdx Qdy  1, 2 3 ( , ) L L L D 对 来说为正方向 L L1 L2 L3 D D1 D2 D3

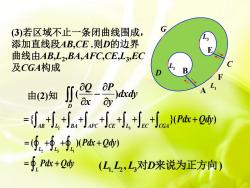
G(3)若区域不止一条闭曲线围成L3添加直线段AB.CE.则D的边界E曲线由AB,L,,BA,AFC,CE,L3,ECc及CGA构成2BDFapLiaQA)dxdy由(2)知axayD=J+J+J+Jarc++J+Je+I(Pdx + Qdy)=(, +9,+, (Pax+ 2d)= d, Pdx +Qdy(L,L2,L,对D来说为正方向）

GD L 3 L 2 F C E L1 A B 由(2) 知 ( ) D Q P dxdy x y   −    2 3 { }( ) AB L BA AFC CE L EC CGA = + + + + + + + + Pdx Qdy         L = + Pdx Qdy  2 3 1 ( )( ) LLL = + + + Pdx Qdy  1, 2 3 ( , ) L L L D 对 来说为正方向 (3)若区域不止一条闭曲线围成， 添加直线段AB ,CE . 则 D的边界 曲线由AB , L 2 ,BA ,AFC,CE , L 3 ,EC 及CGA构成

apaQJ 4、简单应用)dxdy = Φ, Pdx + QdyaxayD(1).简化曲线积分例1 计算I=Φ,e'dx +(xy3 + xe'-2y)dy,其中L为圆周x2+2=2x的正向解 P=e'，Q=xy+xe'-2y山apaQeLy3 +e"ayax02xaqap公.axay由格林公式有 I={[y'dxdy= 0D

解 , y P = e Q xy xe y y 2 3 = + − , y e y P =   y y e x Q = +   3 3 y y P x Q =   −   由格林公式有 3 d d D I y x y = =  2 . 1 例1 3 d ( 2 )d , y y L I e x xy xe y y = + + − 计算  其中L为圆周 x y 2x 2 2 + = 的正向. O x y 0 (1). 简化曲线积分 4、简单应用 ( ) L D Q P dxdy Pdx Qdy x y   − = +    