《高等数学》课程教学资源（课件讲稿，下册）第9章 第1节 多元函数的基本概念

第九章多元函数微分学及其应用人民邮电出版社RISHTPRES

第九章 多元函数微分学及其应用

本章内容多元函数的基本概念0102偏导数与全微分03多元复合函数和隐函数的求导04多元函数的极值05方向导数与梯度06多元复合函数微分学的几何应用

本章内容 01 多元函数的基本概念 02 偏导数与全微分 03 多元复合函数和隐函数的求导 04 多元函数的极值 05 方向导数与梯度 06 多元复合函数微分学的几何应用

9.1多元函数的基本概念人民邮电出版社RISTPRES

9.1 多元函数的基本概念

本节内容01多元函数的概念02二元函数的极限03二元函数的连续性

本节内容 01 多元函数的概念 02 二元函数的极限 03 二元函数的连续性

OA一、多元函数的概念1.区域(1)邻域设P(xo,yo)是xOy平面上的一定点，d是某一正数，与点P(xo,y)的距离小于d 的点P(x,y)的全体，称为点P（x,y）的d 邻域，记为U(P,d),即U(Po,d)= (PllP,Pl <d)亦即x,y)/ /(x- xo)2 +(y- yo)2<U(P.,d) =F

(1)邻域 一、多元函数的概念 1.区域 5

OA、多元函数的概念7在几何上，U(P,d）表示以P（x.，y）为中心，d为半径的圆的内部（不含圆周），如图9.1所示，04图9.1

图 9.1 一、多元函数的概念 6 O x y P0

0O?0一、多元函数的概念上述邻域U(P.d）去掉中心P（xa，y）后，称为P（xo.y）的去心邻域，记作U(Pd），即U(P,d)= fx, )lo <V(x- xo)* +(y- yo) <d如果不需要强调邻域的半径d，则用U(P）表示点P（xo,Jo)的邻域，用U(P）表示点P（xo.y）的去心邻域

一、多元函数的概念 7

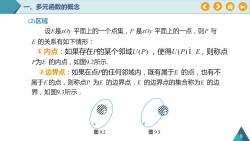
OOA0一、多元函数的概念(2)区域设E是xOy平面上的一个点集，P是xOy平面上的一点，则P与E的关系有如下情形：①内点：如果存在P的某个邻域U(P），使得U(P)iE，则称点P为E的内点，如图9.2所示②边界点：如果在点P的任何邻域内，既有属于E的点，也有不属于E的点，则称点P为E的边界点.E的边界点的集合称为E的边界，如图9.3所示，图9.2图9.3

(2)区域 图 9.2 一、多元函数的概念 8 P E E P 图 9.3

A一、多元函数的概念③开集：如果点集E的每一点都是E的内点，则称E为开集④连通集：设E是平面点集，如果对于E中的任何两点，都可用完全含于E的折线连接起来，则称E是连通集③开区域：连通的开集称为开区域，也称区域6闭区域：开区域连同它的边界称为闭区域?

一、多元函数的概念 9

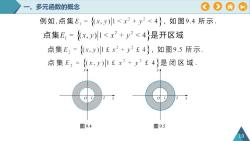
O#A一、多元函数的概念例如，点集E,=(x,)1x2+2<4，如图9.4所示，点集E,=(x,)1x2+2<4是开区域点集E=（x)1x2+4，如图9.5所示点集=（)+24是闭区域.图9.4图9.5

图 9.4 一、多元函数的概念 10 O 1 2 y x O 1 2 y x 图 9.5