《高等数学》课程教学资源（讲稿，上册）第6章习题

习题课O#常微分方程一、一阶微分方程求解二、高阶微分方程的解法

常微分方程 二、高阶微分方程的解法 一 、 一阶微分方程求解 习题课

CAO-、一阶微分方程求解1.一阶标准类型方程求解三个标准类型：可分离变量方程齐次方程一阶线性方程关键：辨瓣别方程类型，掌握求解步骤2.一阶非标准类型方程求解变量代换法

一 、 一阶微分方程求解 1. 一阶标准类型方程求解 关键: 辨别方程类型 , 掌握求解步骤 2. 一阶非标准类型方程求解 变量代换法 三个标准类型: 可分离变量方程, 齐次方程, 一阶线性方程

OOA0二.高阶微分方程的解法1.可降阶的高阶微分方程(1)y(n)=f(x）型的微分方程(2）J"=f(x,y)型的微分方程令y'= p(x)令y'= p(y)(3）J"=f(y,)型的微分方程

二. 高阶微分方程的解法 （1） 型的微分方程 （2） 型的微分方程 ( ) ( ) n y  f x （3） 型的微分方程 y   f (x, y ') y   f (y, y ') 1.可降阶的高阶微分方程 令 y   p ( x ) 令 y   p ( y )

O#二.高阶微分方程的解法2.高阶线性微分方程（1）二阶常系数齐次线性微分方程（2）二阶常系数非齐次线性微分方程

4 2.高阶线性微分方程 二阶常系数齐次线性微分方程 （2) 二阶常系数非齐次线性微分方程 （1） 二. 高阶微分方程的解法

O#O二阶常系数齐次线性微分方程y"+py'+gy=0的通解的求解过程如下(1)将原方程化为标准形式：y"+py'+qy=0写出y+py'+qy=0的特征方程+pr+q=0，求得特征根π5.(2)(3)按照下表得到y"+py+qy=0的通解y"+py+qy=0的通解y"+py'+qy=O的特征根y=Ce" +C,e'sx两个不等的实根ry=(C +C,x)e*两个相等的实根r=r=r两个共轭复根ri2=αtiy=ea*(C,cosβx+C,sinβx)L

5 二阶常系数齐次线性微分方程y   py   qy  0 的通解的求解过程如下： （1） 将原方程化为标准形式：y   py   qy  0. 2 1 2 （2） 写出y   py   qy  0 的特征方程r  pr  q  0，求得特征根r， r . （3） 按照下表得到y   py   qy  0 的通解. y   py   qy  0的特征根 y   py   qy  0的通解 1 2 两个不等的实根r≠r 两个共轭复根r1，2 ＝α±iβ 1 2 两个相等的实根r＝r＝r

OC二阶常系数非齐次线性微分方程y"+ py'+ qy = f(x)1. f(x)= Pm(x)ex型2. f(x)=eax[P(x)cosox+ P,(x)sinx]型6

1. ( ) ( ) e   x m f x P x 型 6 y   py   qy  f ( x) 二阶常系数非齐次线性微分方程 2. ( ) e [ ( ) cos ( )sin ]      x l n f x P x x P x x 型

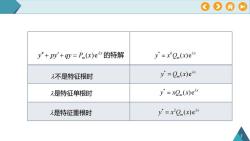
OAy = x*Om(x)exy"+py+qy=P(x)e×的特解y'=Om(x)ear几不是特征根时y" = xOm(x)ear几是特征单根时y = x'Om(x)ear入是特征重根时

7 ( ) e x m y py qy P x       的特解 * ( ) e x m y Q x   * ( ) e k x m y x Q x   * ( ) e x m y xQ x   * 2 ( ) e x m y x Q x   不是特征根时 是特征单根时 是特征重根时

O?O2. f(x)=ex[P(x)cosのx+ P,(x)sinのx]型y"+ py'+qy=e[P(x)cosのx+P,(x)sinのx]，其中P(x)，P(x)分别是关于x的I次和n次多项式，元，の为常数特解可设为=xe[R' (x)cosのx+ R(x)sinx],其中R(x)，R(x）均为m次待定系数的多项式，m=max(l,n特别注意特解中含有2(m+1)个待定实系数；当元+のi不是特征根时，k=0,当a+のi是特征根时，k=18

8 2(m 1)个待定实系数；当  i 不是特征根时，k  0;当  i是特征根时，k  1 . '' ' e [ ( ) cos ( )sin ] ( ) ( )     x l   n  ， l ， n y py qy P x x P x x 其中P x P x 分别是关于x 特解可设为 * 1 2 e [ ( )cos ( )sin ]  y  x k x Rm x x  Rm x x ， 1 2 ( ) ( ) max{ , } Rm m 其中 x ，R x 均为m 次待定系数的多项式，m l n，特别注意特解中含有 2. ( ) e [ ( ) cos ( )sin ]      x l n f x P x x P x x 型 的l次和n次多项式，，为常数

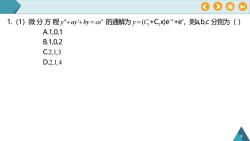
》1.（1）微分方程y"+ay'+by=ce的通解为y=(C,+C,x)e-*+e，则a,b,c分别为（）A.1,0,1B.1,0,2C.2,1,3D.2,1, 4O

9 1 2 '' ' ( 2,1,3 2,1,4      x x x 1.（1）微 分 方 程 y ay by ce 的通解为 y C +C x)e +e ，则a,b,c 分别为（ ） A.1,0,1 B.1,0,2 C. D

OA(2）微分方程y"=4y+8y=e2×(1+cos2x)的特解可设为y=（）A.Ae2x +e2*(Bcos2x+Csin 2x)B.Axe2x +e?*(Bcos2x+Csin 2x)C.Ae2x + xe2*(Bcos2x+C sin 2x)D.Axe2x + xe2*(Bcos 2x+Csin 2x)O

10 ' 2 * 2 2 2 2 2 2 2 2 '' 4 8 (1 cos2 ) ( cos2 sin 2 ) ( cos2 sin 2 ) ( cos2 sin 2 ) ( cos2 sin 2 ) x x x x x x x x x y y y e x Ae e B x C x Axe e B x C x Ae xe B x C x Axe xe B x C x             （2）微分方程 的特解可设为y =（ ) A. B. C. D