《高等数学》课程教学资源（课件讲稿，下册）第9章 第2讲 偏导数与全微分

第二节偏导数与全微分人民邮电出版社RISHTPRES

第二节 偏导数与全微分

本节内容偏导数二、 高阶偏导数三、全微分

本节内容 一、 偏导数 二、 高阶偏导数 三、 全微分

OOAO偏导数1.偏导数的概念设二元函数f(x,y）在点(x：y）的某邻域内有定义，当y固定定义9.5在y.而x在x处有增量Dx时，相应的函数有增量f(x+Dx,y。）-f（xo，Jo）如果极限f(x。+ Dx,yn)-f(xo,yo)limDxDrR 0存在，则称此极限值为函数z=f(x,)在点(xo，y）处关于x的偏导数f1z记为: f(xo,yo),z,(xo. Jo)[x(xo)2I(xn.V)f(x +Dx,yo)- f(xo,yo)即f,(xo,Jo)=limDxDx?0

一、 偏导数 1.偏导数的概念 定义 9.5 3

O?偏导数f(xo,y。+Dy)- f(xo,Jo)存在,则称类似地，如果极限limDyDRO此极限值为函数z=f(x,y)在点(xs，y）处关于y的偏导数.记作12Ifx-xa J,(xo,yo)TyTyX=XX=Xy=yoy=o=Vo

一、 偏导数 4

O?O偏导数的概念可以推广到二元以上的函数，例如,三元函数u=f(x，V,z)在点(x，y,z)处对x的偏导数定义为f(x+Dx ,y,z) - f(x,y,z)Ji(x,y,z)=limDxDx?0f,(x,y,z)=?f.(x, y,2) =?

例如, 三元函数 u = f (x , y , z) 在点 (x , y , z) 处对 x 的 • 偏导数的概念可以推广到二元以上的函数 . 偏导数定义为

一、偏导数O?0若函数z=f(x,y)在区域D内每一点(x,J)处对x偏导数存在，那么这个偏导数就是xy的函数，称它为函数z=f(x,y）对x的偏导函数z 1f记作Ixx2J.(x,).类似地，可以定义函数z=f(x,）对y的偏导函数，1z 1f记作2(ay).注：(I)偏导函数又简称偏导数：(2)偏导数的概念可以推广到二元以上的函数

一、 偏导数 6

、偏导数OAH求二元函数z=f(x,y)偏导数的方法：(1)把视为常数，用一元函数的求导法则求2(2）把x视为常数，用一元函数的求导法则求y求二元函数z=f(x,y)在点(xo.yo)偏导数的方法：(1)一元函数z=f(x,y)在点x处（或z=f(xo:J)在点y。处）的导数;(2) f.(xo,yo)= f (x,y)lr=x J,(xo, yo)= f,(x,y)r-xV

一、 偏导数 7

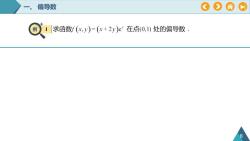
偏导数谷求函数f(x,y)=(x+2y)e在点(0,1)处的偏导数：8

一、 偏导数 例 1 8

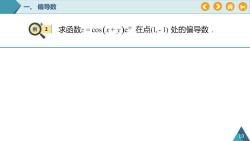
偏导数?求函数z=cos(x+y)e在点(1,-l)处的偏导数

一、 偏导数 例 2 10

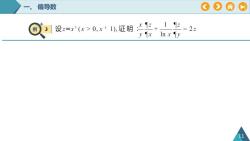
偏导数A1Zx设z=x(x>0,x11),证明OIn x1xV1

一、 偏导数 例 3 11