《高等数学》课程教学资源（课件讲稿）第十章 重积分_1004重积分的应用

重积分第十章第四节重积分的应用曲面的面积工二、质心三、转动惯量四、引力08

第十章 重积分 第四节 重积分的应用

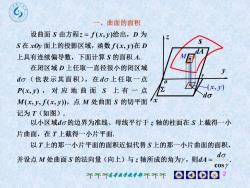
?、曲面的面积设曲面 S 由方程z= f(x,y)给出，D 为ZSS在xOy面上的投影区域，函数f(x,y)在 DdAM上具有连续偏导数，下面计算S的面积A0在闭区域D上任取一直径很小的闭区域yd。（也表示其面积），在do上任取一点0八(x,y)ZP(x,)，对应地曲面S上有一点doIxM(x,J,f(x,y)，点 M 处曲面 S 的切平面记为T（如图）以小区域dα的边界为准线、母线平行于z轴的柱面在S上截得一小片曲面，在T上截得一小片平面以T上的那一小片平面的面积近似代替S上的那一小片曲面的面积do并设点M处曲面S的法向量（向上）与z轴所成的角为，则dAcosy0008个不高教学教学部不不不

高等数学教学部 2 d (x, y) M dA x y z s  o 

Z: n=(-fr(x,y),-f,(x,y),1)SdA1M面cos=/1+ f'(x,y)+ f,(x,y)y.:. dA = /1+ f(x,y)+ f(x,y)do,0V(x,y)W..A= J /1+ f'(x, y)+ f,(x,y)do,do1此为曲面的面积公式若曲面的方程为x =g(y,z),(y,z)e Dyz:. A = [J /1+ g,(y,z)+ g'(y,z)do.若曲面的方程为y= h(z,x),(z,x)e Dx.. A= JI /I+ h(z,x)+h'(z,x)do.Dex008个不不高等数学教学部不不

高等数学教学部 3 n ( f (x, y), f (x, y),1),   x  y   , 1 ( , ) ( , ) 1 cos 2 2 f x y f x y  x  y   1 ( , ) ( , ) , 2 2 dA   f x x y  f y x y d 1 ( , ) ( , ) , 2 2 A f x y f x y d D     x  y 1 ( , ) ( , ) . 2 2 A g y z g y z d Dyz     y  z 1 ( , ) ( , ) . 2 2 A h z x h z x d Dzx     z  x d (x, y) M dA x y z s  o 

例1求球面x2+y2+z2=α2，含在圆柱体x2+y2=ax内部的那部分面积。解 记D: x2+y2≤ax, (y≥0)Zz=/a? -x?- y?北Zr=Va?-x?-y?' 3ya2-x2-yy. A=4[l 1+ z2 + z, dxdyD,X-4小1dxdy21D,cos- 4a" do f pdp = 2元a2 - 4a?a0008个个个高等数学教学部

高等数学教学部 4 , 2 2 2 z  a  x  y x y z A z z dxdy D1 D     x  y 1 2 2 4 1     1 2 2 2 4 D dxdy a x y a           cos 0 2 2 2 0 1 4 a d a a d 2 4 . 2 2  a  a , 2 2 2 a x y x z x     , 2 2 2 a x y y z y    

C例2设有一颗地球同步轨道通信卫星，距地面的高度为h=36000km，运行的角速度与地球自转的角速度相同.试计算该通信卫星的覆盖面积与地球表面积的比值（地球半径R=6400km）+z解建立坐标系如图，通信卫星的覆盖区域为z = R2-x? - y?,x2 + y? ≤ R2 sin2α,R记 D:x’ + y2≤R’ sin’α.这里cosαR+hyJJ /1+z(x,y)+z;(x,y)do:A=XDxyJRRRsinepdpde =f." defdo=zpdpR?R2-x2 -R2-pDxyDxy1hAh~42.5%.= 2元R(1 - cosα) = 2元R24元R22(R + h)R+h'008不不不高等数学教学部不不不

高等数学教学部 5 x y z  o  , sin , 2 2 2 2 2 2 2 z  R  x  y x  y  R  : sin . 2 2 2 2 Dxy x  y  R  A z x y z x y d Dxy     x  y 1 ( , ) ( , ) 2 2 d R x y R Dxy     2 2 2     d d R R Dxy    2 2           sin 0 2 2 2 0 R d R R d 2 (1 cos ) 2  R   2 , 2 R h h R     2 4 R A   2(R h) h    42.5%

二、 质心设在xOv面有n个质点,它们分别位于点(x,y),(xz,y2),.,(xn,yn),质量分别为mj,m2,.…,m,，该质点系对 轴和x轴的静力矩为M,-Zm,x,M,-Zm,yi,i=l-"nLx,m;y,m;i=l该质点系的质心坐标为 x=V="WSmmi1oo8个不不高尊数学教学部不不不

高等数学教学部 6 , , 1 1       n i x i i n i y i i M m x M m y , 1 1      n i i n i i i m x m x . 1 1      n i i n i i i m y m y

设有一平面薄片，占有xov面上的闭区域D，在点(x,)处的面密度为u(x,J)，假定μ(x,y)在D上连续，下面计算平面薄片的质心坐标在闭区域D上任取一直径很小的闭区域dα（也表示其面积），（x，y)是这小区域的一个点薄片中相应于do的部分的质量近似等于μ(x,y)do，这部分质量近似看作集中于点（x，V）上，于是静力矩dM, = xu(x,y)do,dM, = yu(x,y)do,.. M, = [[ xμ(x, y)do, M, = [f yu(x, y)do.0M - JJ μ(x, y)do,而薄片的质量为-J xμ(x, )do] yu(x, y)doD1X=y=所以薄片的质心坐标为JJ u(x, )doJJ u(x, y)do00001018个个个高等数学教学部

高等数学教学部 7 dM x(x, y)d ,dM y(x, y)d , y  x  ( , ) , ( , ) .      D x D M y x x y d M y x y d ( , ) ,   D M  x y d , ( , ) ( , )    D D x y d x x y d x     . ( , ) ( , )    D D x y d y x y d y    

若薄片是均匀的，质心称为形心形心坐标为 x= xdo, =二 ydo, 其中A-=J do.8010108个个个高等数学教学部不不个

高等数学教学部 8 , 1   D xd A x  , 1   D yd A y  .   D 其中A d

例3 求位于两圆p=2sinθ、p=4sin0之间的均匀薄片的质心1解由对称性知x= 0，-JJ yda=Jp'sinodpdo依公式计算V=snsin Adep'dp :x33元2sin000不不个高等数学教学部不不个

高等数学教学部 9 x y C 4 2   D yd A y  1   D  dd  sin 3 1 2            4sin 2sin 2 0 sin 3 1 d d . 3 7 

-三、转动惯量设在xoy面有n个质点，它们分别位于点(xj,.),(x2,y2),.,(xn,y,),质量分别为m1,m2,mn,由力学知道，该质点系对于x轴、y轴的转动惯量为"Wm,xM1,-Zmx,1i=1x :=M21m合000810个不个高数学教学部不不不

高等数学教学部 10 . 1 2   n i y mi xi , I 1 1       n i i n i i i y m m x M M x