《复变函数与积分变换》课程教学课件（PPT讲稿）第四章 解析函数的级数表示 4.3 解析函数的泰勒展开

第三节泰勒级数 一、泰勒定理 二、将函数展成泰勒级数 三、典型例题 四、小结与思考

第三节泰勒级数 一、泰勒定理 二、将函数展成泰勒级数 三、典型例题 四、小结与思考

一、泰勒定理 1.定理4.6设函数f(z)在区域D内解析，z为D内一个点， R为z到D的边界的最短距离，则当z-<R时，f(z)可 展成幂级数，即 f)-Eo(-zr.-eK n=0 其中c,=(》.并且展开式是唯一的 n 则称它为f(z)在z的泰勒展开式，右端的级数为f(z) 在z点的泰勒级数

2 一、泰勒定理 展成幂级数 即 为 到 的边界的最短距离 则当 时 可 定理 设函数 在区域 内解析 为 内一个点 , , , ( ) 1. 4.6 ( ) , , 0 0 0 R z D z z R f z f z D z D −  f z c z z z K n n =  n −   = ( ) ( ) , 0 0 , . ! ( )0 ( ) 其中 并且展开式是唯一的 n f z c n n = . ( ) , ( ) 0 0 在 点的泰勒级数 则称它为 在 的泰勒展开式 右端的级数为 z f z z f z

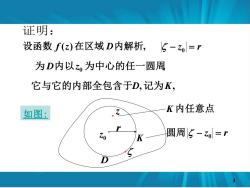
证明： 设函数f(z)在区域D内解析，5-z=r 为D内以z为中心的任一圆周 它与它的内部全包含于D,记为K, 如图： K内任意点 Zo K 圆周5-z0=1

D z K . 内任意点 设函数 f (z)在区域 D内解析, , 为D内以z0 为中心的任一圆周 如图 : r 0 z . K − z = r 圆周  0 .  0  − z = r 它与它的内部全包含于D,记为 K, 3 证明：

由柯西积分公式，有 f(z)= 1f2a5,其中K取正方向. 2niks-z 因为积分变量6取在圆周K上，点z在K的内部， 所以 Z-Zo <1. 5-z0 1 1 则 5-z5-01-z-0 5-z0

由柯西积分公式 , 有  − = K z f i f z d , ( ) 2π 1 ( )    其中 K 取正方向. 因为积分变量 取在圆周K 上,点 z 在 K 的内部, 1. 0 0  − − z z z  所以 0 0 0 1 1 1 1 z z z z z − − − − = −    则 4

1 +2++++ =5-z0 是e-r ue

   + − − + − − + − = 2 0 0 0 0 0 1 ( ) ( ) 1 z z z z z z  z      + − − + n  z z z ( ) 0 0    = + − − = 0 1 0 0 ( ) . ( ) 1 n n n z z  z   − = +  −      − = 1 0 1 0 0 ( ) ( ) ( )d 2π 1 ( ) N n n K n z z z f i f z    于是         − − +  = + K n N n n z z z f i ( ) d . ( ) ( ) 2π 1 1 0 0    5

由高阶导数公式，上式又可写成 e-空贤e-r+a 1=0 英风a-2知三ge-r5 若lim Ry(z)=0, N->oo 可知在内@/-y n!

由高阶导数公式, 上式又可写成  − = = − + 1 0 0 0 ( ) ( ) ( ) ! ( ) ( ) N n N n n z z R z n f z f z 其中         − − =  = + K n N n N n z z z f i R z    ( ) d ( ) ( ) 2π 1 ( ) 1 0 0 lim ( ) = 0, → R z N N 若 可知在K内   = = − 0 0 0 ( ) ( ) ! ( ) ( ) n n n z z n f z f z 6

即f(z)在K内可以用幂级数来表示， 令 - 0=z- 5- 0=q q是与积分变量5无关的量，且0≤q<1, f(z)在D(KcD)内解析，则在K上连续， 因此f(5)在K上也连续，f(5)在K上有界

即 f (z)在 K 内可以用幂级数来表示, 令 q r z z z z z = − = − − 0 0 0  f (z)在 D (K  D)内解析, 则在K上连续, q 是与积分变量 无关的量, 且0  q  1, 因此 f ( )在 K 上也连续, f ( )在 K 上有界, 7

即存在一个正常数M,在K上f(5)≤M. R,age-u n s,1.M 2r=9 2πr 21-q

即存在一个正常数M, 在K上 f ( )  M. z z s z f R z K n N n N n ( ) d ( ) ( ) 2π 1 ( ) 1 0 0    = + − −              − − −   K n=N n s z z z z f d ( ) 2π 1 0 0  0     =      n N n q r r M 2 2 1 . 1 q Mq N − = 8

Iimq”=0→lim Ry(z)=0在K内成立， N->oo N> 从而在K内 泰勒级数 n=0 n! f(z)在z的泰勒展开式， 说明： (1)从证明可知，函数f(z)在z处的幂级数的收敛 半径至少等于从z到D的边界上点的最短距离

lim = 0 → n N q lim ( ) = 0 K → R z N N 在 内成立, 从而在K内   = = − 0 0 0 ( ) ( ) ! ( ) ( ) n n n z z n f z f z f (z) 在 z0 的泰勒展开式, 泰勒级数 9 说明： . (1) , ( ) 0 0 半径至少等于从 到 的边界上点的最短距离 从证明可知 函数 在 处的幂级数的收敛 z D f z z

(2)如果函数f(z)在D内有奇点a,则使f(z)在z的 泰勒展开式成立的R,等于从z到f(z)的距z最近 的一个奇点a之间的距离，即R=a-o (3)函数f(z)在z处的泰勒展开式是惟一的 设f(z)在。已被展开成幂级数： f(2)=a+a(z-2o)+a2(z-2)2+. +an(2-2o)”+., 10

, . , ( ) (2) ( ) , ( ) 0 0 0 0 a R a z R z f z z f z D a f z z 的一个奇点 之间的距离 即 = − 泰勒展开式成立的 等于从 到 的距 最近 如果函数 在 内有奇点 则使 在 的 (3) ( ) . 函数f z 在z0 处的泰勒展开式是惟一的 10 ( ) : 设 f z 在 z0 已被展开成幂级数 f (z) = a0 + a1 (z − z0 ) + a2 (z − z0 ) 2 + ( ) , + an z − z0 n +