《概率论与数理统计》课程教学资源(知识点与公式)概率论与数理统计公式全集

概率论与数理统计公式全集 一、随机事件和概率 1、随机事件及其概率 运算律名称 表达式 交换律 A+B=B+A AB=BA 结合律 (A+B)+C=A+(B+C)=A+B+C (AB)C=A(BC)=ABC 分配律 AB±C)=AB±AC A+(BC)=(A+BXA+C) 德摩根律 A+B=AB 4B=4+B 2、概率的定义及其计算 公式名称 公式表达式 求逆公式 P(=1-P(A0 加法公式 P氏A+B)=PA)+PB-P氏AB) 条件概率公式 P()PAB) P(A) 乘法公式 P(AB)=P(A)P(BA)P(AB)=P(B)P(AB) 全概率公式 -4m4 贝叶斯公式 PA)PE4) P(A,B)=- (逆概率公式) 44 伯努利概型公式 P.(k)=Chp(I-p)"-k,k=0.L.n 两件事件相互独立相PAB)=PAP(B);P代A)=PB);PA=P;P)+PEA=1; 应公式 P(B)+P(B)=1
1 概率论与数理统计公式全集 一、随机事件和概率 1、随机事件及其概率 运算律名称 表达式 交换律 A+ B = B+ A AB= BA 结合律 (A+ B) +C = A+ (B +C) = A+ B +C (AB)C = A(BC) = ABC 分配律 A(B C) = AB AC A+ (BC) = (A+ B)(A+C) 德摩根律 A+ B = AB AB = A+ B 2、概率的定义及其计算 公式名称 公式表达式 求逆公式 P(A) =1− P(A) 加法公式 P(A+ B) = P(A) + P(B) − P(AB) 条件概率公式 ( ) ( ) ( ) P A P AB P B A = 乘法公式 P(AB) = P(A)P(B A) P(AB) = P(B)P(AB) 全概率公式 = = n i P B P Ai P B Ai 1 ( ) ( ) ( ) 贝叶斯公式 (逆概率公式) = = 1 ( ) ( ) ( ) ( ) ( ) i j i j j j P A P B A P A P B A P A B 伯努利概型公式 P k C p p k n k k n k n ( ) = n (1− ) − , = 0,1, 两件事件相互独立相 应公式 P(AB) = P(A)P(B) ; P(B A) = P(B) ; P(B A) = P(B A) ; P(B A) + P(B A) =1 ; P(B A) + P(B A) =1

二、随机变量及其分布 1、分布函数性质 P(X≤b)=F(b)P(a中 =ae40 Γ0,其他 正态分布N4,G),G>0 w2a -<x<+ Awa器a, D(x)= 标准正态分布N(O,1) m房。背 -0<r<+d0
2 二、随机变量及其分布 1、分布函数性质 P(X b) = F(b) P(a X b) = F(b) − F(a) 2、离散型随机变量 分布名称 分布律 0–1 分布 B(1, p) ( ) (1 ) , 0,1 1 = = − = − P X k p p k k k 二项分布 B(n, p) P X k C p p k n k k n k n ( = ) = (1− ) , = 0,1, , − 泊松分布 P()或() , 0,1,2, ! ( = ) = = − k k P X k e k 几何分布 G( p) P(X = k) = (1− p) k−1 p, k = 0,1,2, 超几何分布 H(N,M,n) ( ) , k l,l 1, ,min( n,M ) C C C P X k n N n k N M k = = M = + − − 3、连续型随机变量 分布名称 密度函数 分布函数 均匀分布 U (a,b) = − 0, 其他 , 1 ( ) a x b f x b a − − = x b a x b b a x a x a F x 1, , 0, ( ) 指数分布 ( 0) 1 ( )或 ( ), = E E = − 0, 其他 , 0 ( ) e x f x x − = − 1 , 0 0, 0 ( ) e x x F x x 正态分布 ( , ), 0 2 N = − + − − f x e x x 2 2 2 ( ) 2 1 ( ) − − − = x t F x e d t 2 1 ( ) 2 2 2 ( ) 标准正态分布 N(0,1) = − + − x e x x 2 2 2 1 ( ) − − − = x t x e dt 2 1 ( ) 2 2 2 ( )

三、多维随机变量及其分布 1、离散型二维随机变量边缘分布 P=PX=)=∑PX=Y=y)=∑Pg p=PW=y)=∑PX=,Y=y)=∑P 2、离散型二维随机变量条件分布 P=x=水==PX-=2.=2 P(Y=y P%=AT-yK=-是/=2 P(X=x) 3、连续型二维随机变量(X,P)的联合分布函数Fx,)=∫fu,d 4、连续型二维随机变量边缘分布函数与边缘密度函数 边缘分布函数:Fx()=广fu,dha边缘密度函数:r)=fxd F)=[f(u.v)dudv f(y)=[f(u.y)du 5、二维随机变量的条件分布 m0器nmwn8en
3 三、多维随机变量及其分布 1、离散型二维随机变量边缘分布 = = = = = = j j i i i j pij p P(X x ) P(X x ,Y y ) = = = = = = i i j j i j pij p P(Y y ) P(X x ,Y y ) 2、离散型二维随机变量条件分布 , 1,2 ( ) ( , ) ( ) = = = = = = = = = i P p P Y y P X x Y y p P X x Y y j ij j i j i j i j , 1,2 ( ) ( , ) ( ) = = = = = = = = = j P p P X x P X x Y y p P Y y X x i ij i i j j i j i 3、连续型二维随机变量( X ,Y )的联合分布函数 − − = x y F(x, y) f (u,v)dvdu 4、连续型二维随机变量边缘分布函数与边缘密度函数 边缘分布函数: − + − = x FX (x) f (u,v)dvdu 边缘密度函数: + − f x = f x v dv X ( ) ( , ) − + − = y FY (y) f (u,v)dudv + − fY ( y) = f (u, y)du 5、二维随机变量的条件分布 = − y + f x f x y f y x X Y X , ( ) ( , ) ( ) = − x + f y f x y f x y Y X Y , ( ) ( , ) ( )

四、随机变量的数字特征 1、数学期望 离散型随机变量:B)=之:连续型随机变量:B()-达 2、数学期望的性质 (1)E(C=C,c为常数 (X=E(X)E(CX)=CE(X) (②)EX±n=Ex)±E(Y)E(ax±=a0±bEGX+.C,X,)=CX)+C,EX,) (3)若X,Y相互独立则:)=x) (4)IE(XF sE(xE) 3、方差计算公式:D(X)=Ex)-E2() 4、方差的性质 (1)D(C)=0 DD(X)1=0 D(ax+b)=aD(x)DX)<E(X-C) (②)Dx±n=0+Dmt2Cmx,n若X,Y相互独立则:Dx±n=D)+Dn 5、协方差:Com(X,)=EX,)-EXE)若X,Y相互独立则:ComX,)=0 6、相关系数:n品若,Y相互發立则:即V不相关 7、协方差和相关系数的性质 (1)CoMx.X)=D(X)CoMX.r)=ConY.x) (2)CorXj+X2.Y)=CorX1.Y)+CoMX2.Y)Cor(aX+c.bY+d)=abCoMX.Y)
4 四、随机变量的数字特征 1、数学期望 离散型随机变量: + = = 1 ( ) k k pk E X x 连续型随机变量: + − E(X ) = xf (x)dx 2、数学期望的性质 (1) E(C) = C,C为常数 E[E(X)] = E(X) E(CX) = CE(X) (2) E(X Y) = E(X) E(Y) E(aX b) = aE(X) b ( ) ( ) ( ) E C1X1 +CnXn = C1E X1 +CnE Xn (3)若 X,Y 相互独立则: E(XY) = E(X)E(Y) (4) [ ( )] ( ) ( ) 2 2 2 E XY E X E Y 3、方差计算公式: ( ) ( ) ( ) 2 2 D X = E X − E X 4、方差的性质 (1) D(C) = 0 D[D(X)] = 0 ( ) ( ) 2 D aX b = a D X 2 D(X) E(X −C) (2) D(X Y) = D(X) + D(Y) 2Cov(X,Y) 若 X,Y 相互独立则: D(X Y) = D(X) + D(Y) 5、协方差: Cov(X,Y) = E(X,Y) − E(X)E(Y) 若 X,Y 相互独立则: Cov(X,Y) = 0 6、相关系数: ( ) ( ) ( , ) ( , ) D X D Y Cov X Y XY = X Y = 若 X,Y 相互独立则: XY = 0 即 X,Y 不相关 7、协方差和相关系数的性质 (1) Cov(X, X) = D(X) Cov(X,Y) = Cov(Y, X) (2) ( , ) ( , ) ( , ) Cov X1 + X2 Y = Cov X1 Y +Cov X2 Y Cov(aX + c,bY + d) = abCov(X,Y)
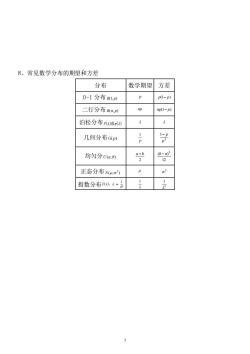
8、常见数学分布的期望和方差 分布 数学期望方差 0-1分布1P) P(l-p) 二行分布BmP) m1-p) 泊松分布减a) 几何分布Gp) 导 均匀分Ua,b) 正态分布N4,a 02 指数分布元-日 5
5 8、常见数学分布的期望和方差 分布 数学期望 方差 0-1 分布 B(1, p) p p(1− p) 二行分布 B(n, p) np np(1− p) 泊松分布 P()或() 几何分布 G( p) p 1 2 1 p − p 均匀分 U(a,b) 2 a + b 12 ( ) 2 b − a 正态分布 ( , ) 2 N 2 指数分布 1 E( ), = 1 2 1

五、大数定律和中心极限定理 1、切比雪夫不等式 若B0=4.)=g,对于任意E>0有P叫x-B≤D”或PK-EX0的独立同分布时,当n充分 大时有: 立x-刚 二→NO, (2)拉普拉斯定理:随机变量nm=l2)-mp)则对任意X有: 血=应= 《③)近似计算:a2n兴:空当-爱
6 五、大数定律和中心极限定理 1、切比雪夫不等式 若 ( ) , ( ) , 2 E X = D X = 对于任意 0 有 2 ( ) { ( ) } D X P X − E X 或 2 ( ) { ( ) } 1 D X P X − E X − 2、大数定律:若 X1Xn 相互独立且 n → 时, = = ⎯⎯→ n i i D n i i E X n X n 1 1 ( ) 1 1 (1)若 X1Xn 相互独立, 2 ( ) , ( ) E Xi = i D Xi = i 且 i M 2 则: = = ⎯→ → n i i P n i i E X n n X n 1 1 ( ),( ) 1 1 (2)若 X1Xn 相互独立同分布,且 E Xi = i ( ) 则当 n → 时: ⎯→ = P n i Xi n 1 1 3、中心极限定理 (1)独立同分布的中心极限定理:均值为 ,方差为 0 2 的独立同分布时,当 n 充分 大时有: (0,1) 1 ~ N n X n Y n k k n ⎯→ − = = (2)拉普拉斯定理:随机变量 (n 1,2 ) ~ B(n, p) n = 则对任意 x 有: − − →+ = = − − x t n x x e dt x np p np P ( ) 2 1 } (1 ) lim { 2 2 (3)近似计算: ( ) ( ) ( ) ( ) 1 1 n a n n b n n b n n X n n a n P a X b P n k k n k k − − − − − − = = =

六、数理统计 1、总体和样本 总体x的分布函数F国样本X,XX)的联合分布为F)=F) 2、统计量 0样本平均值:-空x2)样本方差:s产2以-矿2的 (同样本标准起:5一2一疗国样本4阶股信面,人-之4以 (6份样本阶中心距:&M-2-矿k-2 3、三大抽样分布 (1)x分布:设随机变量x,X,X,相互独立,且都服从标准正态分布NO),则随机变 量x2=x好+x+.x所服从的分布称为自由度为n的x2分布,记为x2~x2 性质:①x2=mDx2(1=2n②设x~x2m,y~x2m)且相互独立,则x+Y~x2m+m (②,分布:设随机变量x-N0~,且X与Y独立。则随机变量:T赢所服从 的分布称为自由度的m的:分布,记为T~m 性质:0aaMa点oa2=0-a合:学 (③)F分布:设随机变量U-a-tm,且u与独立,则随机变量心-会所 服从的分布称为自由度(m,)的F分布,记为F~Fm,) 性质:设X~Fmm,则~Fm,m)
7 六、数理统计 1、总体和样本 总体 X 的分布函数 F(x) 样本 ( , ) X1 X2Xn 的联合分布为 ( , ) ( ) 1 1 2 k n k n F x x x F x = = 2、统计量 (1)样本平均值: = = n i Xi n X 1 1 (2)样本方差: = = − − − = − = n i i n i i X nX n X X n S 1 2 2 1 2 2 ( ) 1 1 ( ) 1 1 (3)样本标准差: = − − = n i Xi X n S 1 2 ( ) 1 1 (4)样本 k 阶原点距: , 1,2 1 1 = = = X k n A n i k k i (5)样本 k 阶中心距: = = = − = n i k k k i X X k n B M 1 ( ) , 2,3 1 3、三大抽样分布 (1) 2 分布:设随机变量 X1 X2Xn , 相互独立,且都服从标准正态分布 N(0,1) ,则随机变 量 2 2 2 2 1 2 = X + X +Xn 所服从的分布称为自由度为 n 的 2 分布,记为 ~ ( ) 2 2 n 性质:① E[ (n)] n,D[ (n)] 2n 2 2 = = ②设 ~ ( ), ~ ( ) 2 2 X m Y n 且相互独立,则 ~ ( ) 2 X +Y m+ n (2) t 分布:设随机变量 ~ (0,1), ~ ( ) 2 X N Y n ,且 X 与 Y 独立,则随机变量: Y n X T = 所服从 的分布称为自由度的 n 的 t 分布,记为 T ~ t(n) 性质:① ,( 2) 2 [ ( )] 0, [ ( )] − = = n n n E t n D t n ② 2 2 2 ( ) 2 1 lim ( ) (0,1) − − → = = x n t n N e (3) F 分布:设随机变量 ~ ( ), ~ ( ) 2 2 1 2 U n V n ,且 U 与 V 独立,则随机变量 2 1 1 2 ( , ) V n U n F n n = 所 服从的分布称为自由度 ( , ) n1 n2 的 F 分布,记为 ~ ( , ) F F n1 n2 性质:设 X ~ F(m,n) ,则 ~ ( , ) 1 F n m X

七、参数估计 1、参数估计 (1)定义:用(x,X2.x)估计总体参数0,称x.X2.x)为0的估计量,相应的 (X,X2,X,)为总体的估计值。 (2)当总体是正态分布时,未知参数的矩估计值=未知参数的最大似然估计值 2、点估计中的矩估计法:(总体矩=样本矩) 离敬型样本约值:一0-空 连续型样本均值:灭=)=x,0h 离散型参数:-之 3、点估计中的最大似然估计 最大似然估计法:X,X2,.xn取自x的样本,设x~fx,或Px=X)=P)则可得到概率 密度:f%-/,9或X=X.X,=-Px=)=·Bo例1 基本步骤: ①似然函数: 40=1.01或0Bo1 ②取对数:hL=nx,) ③解方程:-0-0最后得:a-00
8 七、参数估计 1、参数估计 (1) 定义:用 ( , , ) X1 X2 Xn 估计总体参数 ,称 ( , , ) X1 X2 Xn 为 的估计量,相应的 ( , , ) X1 X2 Xn 为总体 的估计值。 (2) 当总体是正态分布时,未知参数的矩估计值=未知参数的最大似然估计值 2、点估计中的矩估计法:(总体矩=样本矩) 离散型样本均值: = = = n i Xi n X E X 1 1 ( ) 连续型样本均值: X E X xf x dx + − = ( ) = ( ,) 离散型参数: = = n i Xi n E X 1 2 1 2 ( ) 3、点估计中的最大似然估计 最大似然估计法: X X Xn , , 1 2 取自 X 的样本,设 X ~ f (x,)[ P(X X ) P()] 或 = i = 则可得到概率 密度: ( , , , ) ( , )[ ( , , ) ( ) ( )] 1 1 1 2 1 1 2 = = = = = = = = = n i i n i n n i n i f x x xn f xi 或P X X X X x P X x P 基本步骤: ①似然函数: ( ) ( , )[ ( )] 1 1 = = = n i i n i L f xi 或 P ②取对数: = = n i Xi L f 1 ln ln ( ,) ③解方程: 0 ln 0, , ln 1 = = k L L 最后得: ( , , ), , ( , , ) 1 1 1 2 n k k 1 2 n x x x x x x = =
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《概率论与数理统计》课程教学资源(知识点与公式)概率论与数理统计概率部分知识点总结.doc
- 《概率论与数理统计》课程教学资源(PPT课件)第8章 假设检验 第一节 假设检验.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第8章 假设检验 第二节 正态总体均值的假设检验.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第8章 假设检验 第三节 正态总体方差的假设检验.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第8章 假设检验 第六节 分布拟合检验.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第7章 参数估计 第一节 点估计.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第7章 参数估计 第三节估计量的评选标准.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第7章 参数估计 第四节区间估计.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第7章 参数估计 第五节 正态总体均值与方差的区间估计.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第7章 参数估计 第七节 单侧置信区间.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第6章 样本及抽样分布 第一节随机样本.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第6章 样本及抽样分布 第二次 抽样分布.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第5章 大数定律及中心极限定理 第一节 大数定律.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第5章 大数定律及中心极限定理 第二节 中心极限定理.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第4章 随机变量的数字特征 第一节数学期望.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第4章 随机变量的数字特征 第二节方差.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第4章 随机变量的数字特征 第三节协方差及相关系数.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第4章 随机变量的数字特征 第四节矩,协方差矩阵.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第3章 多维随机变量及其分布 第一节二维随机变量.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第3章 多维随机变量及其分布 第二节 边缘分布.ppt
- 《高等数学》课程教学资源(单元测验)第1-7章单元测验(附答案).doc
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第一章 复数与复变函数 1.5 复变函数的概念.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第一章 复数与复变函数 1.4 无穷大.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第一章 复数与复变函数 1.3 平面点集.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第一章 复数与复变函数 1.2 复数的表示.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第一章 复数与复变函数 1.1 复数.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第二章 解析函数 2.3 复变初等函数.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第二章 解析函数 2.2 解析函数与调和函数的关系.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第二章 解析函数 2.1 解析函数.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第三章 复变函数的积分 3.4 高阶导数公式.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第三章 复变函数的积分 3.3 柯西积分公式.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第三章 复变函数的积分 3.2 柯西积分定理.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第三章 复变函数的积分 3.1 复积分概述.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第四章 解析函数的级数表示 4.4 解析函数的洛朗展开.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第四章 解析函数的级数表示 4.3 解析函数的泰勒展开.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第四章 解析函数的级数表示 4.2 幂级数.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第四章 解析函数的级数表示 4.1 复数项级数.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第五章 留数及其应用 5.4 对数留数与辐角原理.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第五章 留数及其应用 5.3 留数在积分计算中的应用.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第五章 留数及其应用 5.2 留数及留数定理.ppt
