《概率论与数理统计》课程教学资源（PPT课件）第4章 随机变量的数字特征 第一节数学期望

概车纶与款理统外 第四章 随机变量的数字特征 分布函数能完整地描述随机变量的统计特 性，但实际应用中并不都需要知道分布函数而 只需知道随机变量的某些特征. 例如： 判断棉花质量时，既看纤维的平均长度 又要看纤维长度与平均长度的偏离程度 平均长度越长，偏离程度越小，质量就越好；

第四章 随机变量的数字特征 分布函数能完整地描述 随机变量的统计特 性, 但实际应用中并不都需要知道分布函数而 只需知道 随机变量的某些特征. 判断棉花质量时, 既看纤维的平均长度 平均长度越长,偏离程度越小, 质量就越好; 又要看 纤维长度与平均长度的偏离程度 例如：

概率伦与款理统外 考察一射手的水平，既要看他的平均环数是否 高，还要看他弹着点的范围是否小，即数据的波动 是否小. 由上面例子看到，与随机变量有关的某些数 值，虽不能完整地描述随机变量，但能清晰地描 述随机变量在某些方面的重要特征，这些数字特 征在理论和实践上都具有重要意义。 本章主要内容 数学期望、方差、协方差、相关系数、矩

考察一射手的水平, 既要看他的平均环数是否 高, 还要看他弹着点的范围是否小, 即数据的波动 是否小. 由上面例子看到，与随机变量有关的某些数 值，虽不能完整地描述随机变量，但能清晰地描 述随机变量在某些方面的重要特征 ,这些数字特 征在理论和实践上都具有重要意义. 本章主要内容 数学期望、方差、协方差、相关系数、矩

概车纶与款理统外 第一节 数学期望 一、数学期望的概念 二、随机变量函数的数学期望 三、数学期望的性质

一、数学期望的概念 三、数学期望的性质 二、随机变量函数的数学期望 第一节 数学期望

一、数学期望的概念 1数学期望的由来 分赌本问 题 100法郎 甲 乙 德梅尔 甲赢了两 乙赢了一局 局

德•梅尔 一、数学期望的概念 1.数学期望的由来 100法郎 甲 乙 甲赢了两 乙赢了一局 局 分赌本问 题

1.数学期望的由来 分赌本 问题 德梅尔 帕斯卡 费马

分赌本 问题 德•梅尔 1.数学期望的由来 帕斯卡 费马

设想继续赌下去，至多再赌两局必可 决出胜负。 因为其结果必为以下四种 情况之尸 第 局 第二局 甲获得100法郎的可能性为3/4，获得0法郎的可 能性为1/4

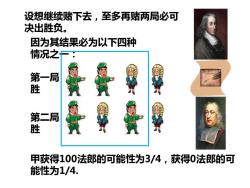
设想继续赌下去，至多再赌两局必可 决出胜负。 因为其结果必为以下四种 情况之一： 第一局 胜 第二局 胜 甲获得100法郎的可能性为3/4，获得0法郎的可 能性为1/4

设随机变量X表示甲最终获得的法郎数 慨率论诞 生！ 则X的分布律为 X 0 100 1 3 4 4 “期望”所得 应为：1 惠更斯 3 0×二+100x-=75(法 4 4 郎) 均值 即X的所有可能取值与其概率之 数学期 为 积的累加， 望

设随机变量 X 表示甲最终获得的法郎数， X P 0 100 1 4 3 4 则 X 的分布律为 “期望”所得 应为： 1 3 0 100 75 4 4  +  = (法 郎), 即 为 的所有可能取值与其概率之 积的累加. X 惠更斯 数学期 望 概率论诞 生！ 均值

概華伦与款程统外 2.离散型随机变量的数学期望 定义设离散型随机变量X的分布律为 P{X=x}=Pk,k=1,2,. 若级数∑xP,绝对收敛，则称级数 ∑sP& k k=1 的和为随机变量X的数学期望，记为E(X).即 E(X=∑P

2. 离散型随机变量的数学期望 定义 ( ) . , ( ). , { } , 1,2, . 1 1 1     =  =  = = = = = k k k k k k k k k k k E X x p X E X x p x p P X x p k X 的和为随机变量 的数学期望 记为 即 若级数 绝对收敛 则称级数 设离散型随机变量 的分布律为 

概车纶与款理统外 关于定义的几点说明 ()EX)是一个实数，而非变量，它是一种加 权平均，与一般的平均值不同，它从本质上体现 了随机变量X取值的真正的平均值，也称均值. (2)级数的绝对收敛性保证了级数的和不 随级数各项次序的改变而改变，之所以这样要 求是因为数学期望是反映随机变量X取可能值 的平均值，它不应随可能值的排列次序而改变

关于定义的几点说明 (1) E(X)是一个实数,而非变量,它是一种加 权平均,与一般的平均值不同 , 它从本质上体现 了随机变量 X 取值的真正的平均值, 也称均值. (2) 级数的绝对收敛性保证了级数的和不 随级数各项次序的改变而改变 , 之所以这样要 求是因为数学期望是反映随机变量X 取可能值 的平均值,它不应随可能值的排列次序而改变

概華论与款程统外 X12 假设 0.020.98 随机变量X的算术平均值为 1+2-1.5, 2 随机变量X的期望为E(X)=1×0.02+2×0.98=1.98. 它从本质上体现了随机变量X取值的平均程度

x O • 随机变量 X 的算术平均值为 1.5, 2 1 2 = + 假设 E(X) = 1 0.02 + 2 0.98= 1.98. 它从本质上体现了随机变量X 取值的平均程度. • 1 • 2 • • X 1 2 p 0.02 0.98 随机变量 X 的期望为