《概率论与数理统计》课程教学资源（PPT课件）第3章 多维随机变量及其分布 第三节 条件分布

第三节 条件分布 一、离散型随机变量的条件分布 二、连续型随机变量的条件分布

一、离散型随机变量的条件分布 二、连续型随机变量的条件分布 第三节 条件分布

、离散型随机变量的条件分布 问题 考虑一大群人，从其中随机挑选一个人，分别 用X和Y记此人的体重和身高，则X和Y都是随 机变量，他们都有自己的分布： 现在如果限制Y 取值从1.5m到1.6m, 在这个限制下求X的 分布

问题 一、离散型随机变量的条件分布 , . , , , 机变量 他们都有自己的分布 用 和 记此人的体重和身高 则 和 都是随 考虑一大群人 从其中随机挑选一个人 分别 X Y X Y . 1.5m 1.6m, 分布 在这个限制下求 的 取值从 到 现在如果限制 X Y

定义设(X,Y)是二维离散型随机变量对于固定 的，若PY=y}>0,则称 P(X=xY-) P(X=xi,Y=yi3Pi P(Y=yi P.j 为在Y=y条件下随机变量X的条件分布律 对于固定的i,若P{X=x}>0,则称 P PY-X-PX-xY- P(X=x) 卫o 为在X=x,条件下随机变量Y的条件分布律 其中i,j=1,2

. , { } { , } { } , { } 0, ( , ) , 为 在 条件下随机变量 的条件分布律 的 若 则 称 设 是二维离散型随机变量对于固定 Y y X p p P Y y P X x Y y P X x Y y j P Y y X Y j j ij j i j i j j = = = = = = = = =  • . , { } { , } { } , { } 0, 为 在 条件下随机变量 的条件分布律 对于固定的 若 则 称 X x Y p p P X x P X x Y y P Y y X x i P X x i i ij i i j j i i = = = = = = = = =  • 其中i, j = 1,2,  . 定义

例1在一汽车工厂中，一辆汽车有两道工序是 由机器人完成的.其一是紧固3只螺栓，其二是 焊接2处焊点.以X表示螺栓紧固得不良的数 目，以Y表示焊点焊接得不良的数目.据积累的 资料知(X,Y)具有分布律： 比 0 1 2 3 P(Y=j) 0 0.840 0.030 0.020 0.010 0.900 1 0.060 0.010 0.008 0.002 0.080 2 0.010 0.005 0.004 0.001 0.020 P(X=i 0.910 0.045 0.032 0.013 1.000

X Y 0 1 2 3 0.840 0.030 0.020 0.010 0.060 0.010 0.008 0.002 2 0.010 0.005 0.004 0.001 1 0 0.900 0.080 0.020 P{X = i} 0.910 0.045 0.032 0.013 1.000 P{Y = j} ( , ) : , . 2 . . 3 , , 资料知 具有分布律 目 以 表示焊点焊接得不良的数目 据积累的 焊接 处焊点 以 表示螺栓紧固得不良的数 由机器人完成的 其一是紧固 只螺栓 其二是 在一汽车工厂中 一辆汽车有两道工序是 X Y Y X 例1

()求在X=1的条件下，Y的条件分布律； (2)求在Y=0的条件下，X的条件分布律， 解在X=1的条件下，Y的条件分布律为 Y=k 0 2 6 2 P(Y=kX=1) 9 9 9 X 0 1 2 3 P(Y=j) 0 0.840 0.030 0.020 0.010 0.900 1 0.060 0.010 0.008 0.002 0.080 2 0.010 0.005 0.004 0.001 0.020 P(X=i 0.910 0.045 0.032 0.013 1.000

(2) 0 , . (1) 1 , ; 求在 的条件下 的条件分布律 求在 的条件下 的条件分布律 Y X X Y = = 解 X Y 0 1 2 3 0.840 0.030 0.020 0.010 0.060 0.010 0.008 0.002 2 0.010 0.005 0.004 0.001 1 0 0.900 0.080 0.020 P{X = i} 0.910 0.045 0.032 0.013 1.000 P{Y = j} 在 X =1的条件下,Y 的条件分布律为 Y = k P{Y = k X = 1} 0 1 2 9 1 9 2 9 6

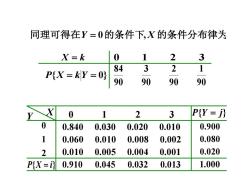
同理可得在Y=0的条件下，X的条件分布律为 X=k 0 1 2 3 84 3 2 1 PiX=kY=0 90 90 90 90 X 0 1 2 3 P(Y=j) 0 0.840 0.030 0.020 0.010 0.900 1 0.060 0.010 0.008 0.002 0.080 2 0.010 0.005 0.004 0.001 0.020 P(X=i 0.910 0.045 0.032 0.013 1.000

同理可得在Y = 0的条件下,X 的条件分布律为 X = k P{X = kY = 0} 0 1 2 3 90 1 90 2 90 3 90 84 X Y 0 1 2 3 0.840 0.030 0.020 0.010 0.060 0.010 0.008 0.002 2 0.010 0.005 0.004 0.001 1 0 0.900 0.080 0.020 P{X = i} 0.910 0.045 0.032 0.013 1.000 P{Y = j}

例2一射手进行射击，击中目标的概率为p(0<p<1) 射击到击中目标两次为止.设 以X表示首次击中目标所进行的射击次数， 以Y表示总共进行的的射击次数. 试求X和Y的联合分布律及条件分布律。 解 P{X=m,Y=n心=pp(1-p)(1-p).(1-p) (n-2)个 即得X和Y的联合分布律为 P{X =m,Y=n)p'g"-2, 其中q=1-p,n=2,3,;m=1,2,.,n-1

例2 一射手进行射击,击中目标的概率为p(0<p<1), 射击到击中目标两次为止.设 以X 表示首次击中目标所进行的射击次数, 以Y 表示总共进行的的射击次数. 试求 X 和 Y 的联合分布律及条件分布律. 解 P{X = m,Y = n} = p  p (1−  p)(1− p)(1− p) (n − 2)个 即得 X 和Y 的联合分布律为 { , } , 2 −2 = = = n P X m Y n p q 其中q = 1 − p, n = 2,3, ; m = 1,2,  ,n − 1

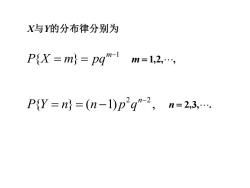
X与的分布律分别为 P{X=m}=pqm1m=1,2, PY=n}=(n-1)p2q”-2,n=23

X与Y的分布律分别为 m = 1,2,  , { } ( 1) , 2 −2 = = − n P Y n n p q n = 2,3,  . 1 { } − = = m P X m pq

所以当n=2,3,.时， P(X=mY=n PX=m,Y=n PY=n p2q"-2 (n-10p2q"-2-n-1’ 当m=1,2,n-1时， P(X=m,Y=n PY=nX=m= PX=m pig"-? =pgw-i, n=m+1,m+2

所以当 n = 2,3,  时, 2 2 2 2 ( 1) − − − = n n n p q p q { } { , } P Y n P X m Y n = = = = , 1 1 − = n 当 m = 1,2,  ,n − 1时, { } { , } P X m P X m Y n = = = = 1 2 2 − − = m n p q p q , − −1 = n m pq n = m + 1,m + 2,  . P{X = mY = n} P{Y = n X = m}

二、连续型随机变量的条件分布 定义设二维随机变量(X,Y)的概率密度为 f(K,y),(X,Y)关于Y的边缘概率密度为，(y)若 对于固定的y人>0，则称fx川为在Y=y fy(y) 的条件下X的条件概率密度记为 f,()=比，y) fy(y)

定义 二、连续型随机变量的条件分布 . ( ) ( , ) ( ) , ( ) ( , ) , ( ) 0, ( , ),( , ) ( ). ( , ) f y f x y f x y X Y y f y f x y y f y f x y X Y Y f y X Y Y Y Y Y X Y =  = 的条件下 的条件概率密度记 为 对于固定的 则 称 为 在 关 于 的边缘概率密度为 若 设二维随机变量 的概率密度为