《概率论与数理统计》课程教学资源（PPT课件）第1章 概率论的基本概念 第五节条件概率

概率伦与敖理统外 第五节 条件概率 一、条件概率 二、乘法定理 三、全概率公式与贝叶斯公式

一、条件概率 二、乘法定理 三、全概率公式与贝叶斯公式 第五节 条件概率

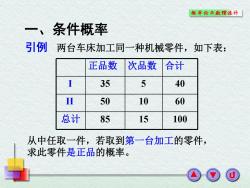
概奉论与散理统计「 一、条件概率 引例 两台车床加工同一种机械零件，如下表： 正品数 次品数 合计 35 5 40 Ⅲ 50 10 60 总计 85 15 100 从中任取一件，若取到第一台加工的零件， 求此零件是正品的概率

引例 两台车床加工同一种机械零件，如下表： 一 、条件概率 正品数 次品数 合计 I 35 5 40 II 50 10 60 总计 85 15 100 从中任取一件，若取到第一台加工的零件， 求此零件是正品的概率

概率论与款理统外 1.定义 设A,B是两个事件，且P(A)>0,称 P(BA)=P(AB) P(A) 为在事件A发生的条件下事件B发生的条件概率. 同理可得 P(AB)=P(AB) P(B) 为事件B发生的条件下事件A发生的条件概率

( ) ( ) ( ) P B P AB 同理可得 P AB  为事件 B 发生的条件下事件 A 发生的条件概率. . ( ) ( ) ( ) , , ( ) 0, 为在事件 发生的条件下事件 发生的条件概率 设 是两个事件 且 称 A B P A P AB P B A A B P A   1. 定义

概奉论与散理统计「 2.性质 (I)非负性：P(BA≥0； (2)规范性：P(SA)=1,P(OA)=0, (3)P(BUB A=P(B A+P(B A)-P(BB.A); (4)P(BA)=1-P(BA) (5)可列可加性：设B1,B2,.是两两不相容的事 件，则有 P084小-2P®

(3) ( ) ( ) ( ) ( ); P B1B2 A P B1 A P B2 A P B1B2 A (4) P(B A) 1 P(B A). (2) 规范性: P(S A) 1, P( A)  0; 件 则有 可列可加性 设 是两两不相容的事 , (5) : , , B1 B2  ( ). 1 1            i i i P Bi A P B A 2. 性质 (1)非负性: P(B A)  0;

概率论与数理统外 例1一个盒子中装有7件产品，包括4件一等品 和3件二等品，从中不放回地取三次，每次取一 件，令A1:第1次取到一等品，=1,2,3 P(A),P(A,A),P(A;A 42)

例1 一个盒子中装有7件产品，包括4件一等品 和3件二等品，从中不放回地取三次，每次取一 件，令 Ai: 第i次取到一等品，i=1,2,3 1 2 1 3 1 2 求 P( A ), P( A A ), P( A A A )

概奉论与散理统计「 二、乘法定理 设P(A)>0,则有P(AB)=P(BA)P(A). 设A,B,C为事件，且P(AB)>0,则有 P(ABC)=P(CAB)P(BA)P(A). 推广设A,A2,.,An为n个事件，n≥2， 且P(A1A,.An-1)>0,则有 P(A1A2.An)=P(AnA1A2.Am-)×1 P(An-4142.An-2)×.×P(A2A)P(A1

( ) ( ) ( ). ( ) ( ) 1 1 2 2 2 1 1 1 2 1 2 1 P A A A A P A A P A P A A A P A A A A n n n n n            且 P(A1A2A n1 )  0, 则有 , , , , 2, 推广 设 A1 A2  An 为 n 个事件 n  设 A,B,C 为事件,且 P(AB)  0, 则有 P(ABC)  P(C AB)P(B A)P(A). 设 P(A)  0, 则有 P(AB)  P(B A)P(A). 二、 乘法定理

概率伦与数理统外 例2某种动物由出生算起活20岁以上的概率为 0.8,活到25岁以上的概率为0.4，如果现在有一个 20岁的这种动物，问它能活到25岁以上的概率是 多少？ 解设A表示“能活20岁以上”的事件， B表示“能活25岁以上”的事件， 则有 P(BA)= P(AB) P(A) 因为P(A=0.8,P(B)=0.4,P(AB)=P(B), 所以P(BA)=PL1B 0.41 P(A) 0.821

例2 某种动物由出生算起活20岁以上的概率为 0.8, 活到25岁以上的概率为0.4, 如果现在有一个 20岁的这种动物, 问它能活到25岁以上的概率是 多少? 设 A 表示“ 能活 20 岁以上 ” 的事件， B 表示 “ 能活 25 岁以上”的事件, 则有 因为 P(A)  0.8, . ( ) ( ) ( ) P A P AB P B A  P(B)  0.4, P(AB)  P(B), . 2 1 0.8 0.4   ( ) ( ) ( ) P A P AB 所以 P B A  解

概奉论与散理统计「 抓阄是否与次序有关？ 例3六个阄，其中一个阄内写着“有” 字，五个阄内不写字，六人依次抓取， 问各人抓到“有”字阄的概率是否相同 解设A表示“第i人抓到有字阉”的事件， i=1,2,3,4,5,6. 则有 P(A)= 1 6

例3 六个阄, 其中一个阄内写着“有” 字， 五个阄内不写字 ，六人依次抓取, 问各人抓到“有”字阄的概率是否相同? 解 i = 1,2,3,4,5,6. 则有 1 1 ( ) , 6 P A = 抓阄是否与次序有关? 设 A 表示“第 i 人抓到有字阄”的事件 , i

概率伦与敖理统外 P(4)=P(44)=P(A)P(A,A) 511 656 P(A)=P(A44)=P(A)P(44)P(444) 5411 6546 依此类推 4)=4)=4)-G 故抓阄与次序无关

2 P(A )= 1 2 P(A A ) 1 2 1 = P(A )P(A A ) 5 1 1 6 5 6    3 1 2 3 1 2 1 3 1 2 P(A ) = P(A A A ) = P(A )P(A A )P(A A A ) 5 4 1 1 6 5 4 6     依此类推 4 5 6 1 ( ) ( ) ( ) . 6 P A  P A  P A  故抓阄与次序无关

概奉论与散理统计「 例4设某光学仪器厂制造的透镜，第一次落下时 打破的概率为1/2，若第一次落下未打破，第二次落 下打破的概率为7/10，若前两次落下未打破，第三 次落下打破的概率为9/10.试求透镜落下三次而未 打破的概率. 解以4，(i=1,2,3)表示事件"透镜第i次落下打破"， 以B表示事件“透镜落下三次而未打破”· 因为B=A1A2A3, 所以P(B)=P(A1A2A)=P(AAA)P(AA)P(A) =a-8a-0u-2-0

例4 设某光学仪器厂制造的透镜, 第一次落下时 打破的概率为1/2,若第一次落下未打破, 第二次落 下打破的概率为7/10 , 若前两次落下未打破, 第三 次落下打破的概率为9/10.试求透镜落下三次而未 打破的概率. 解 以B 表示事件“透镜落下三次而未打破” . , 因为 B  A1 A2 A3 ( ) ( ) 所以 P B  P A1 A2 A3 ( ) ( ) ( )  P A3 A1A2 P A2 A1 P A1 ) 2 1 )(1 10 7 )(1 10 9  (1    . 200 3  以A (i 1,2,3)表示事件"透镜第 i 次落下打破" , i 