《概率论与数理统计》课程教学课件(PPT讲稿)第03章 多维随机变量及其分布 3.2 边缘分布

概率论与数理统外「 第二节 边缘分布 一、边缘分布函数 二、离散型随机变量的边缘分布律 三、连续型随机变量的边缘分布 四、小结
二、离散型随机变量的边缘分布律 三、连续型随机变量的边缘分布 一、边缘分布函数 四、小结 第二节 边缘分布

概率论与散理统计 一、边缘分布函数 问题:已知(X,Y)的分布,如何确定X,Y的分布? ↓ F(x,y)=P{X≤x,Y≤y},F(x)=P{X≤x, P{X≤x=P{X≤x,Y<oo}=F(x,∞)=Fx(x) 0 (X,Y)关于X的边缘分布函数
一、边缘分布函数 F(x, y) P{X x,Y y}, F(x) P{X x}, P{X x} P{X x,Y } F(x,) F (x) X (X,Y)关于X的边缘分布函数. 问 题:已知(X,Y )的分布,如何确定X,Y的分布?

概率论与数理统外】 定义 设F(x,y)为随机变量(X,Y)的分布函数, 则 F(x,y)=P{X≤x,Y≤y}令y→o,称 P{X≤x}=P{X≤x,Y<o∞}=F(x,∞), 为随机变量(X,Y)关于的边缘分布函数 记为Fx(x)=F(x,∞): 同理令x→0, F(y)=F(oo,y)=P{X<o,Y≤y}=P{Y≤y} 为随机变量(X,Y)关于Y的边缘分布函数
F ( y) F( , y) P{X ,Y y} P{Y y} Y 为随机变量 ( X,Y )关于Y 的边缘分布函数. ( , ) . { } { , } ( , ), ( , ) { , } , ( , ) ( , ) , 为随机变量 关 于 的边缘分布函数 则 令 称 设 为随机变量 的分布函数 X Y X P X x P X x Y F x F x y P X x Y y y F x y X Y F (x) F(x,). 记为 X 定义 同理令 x

概率论与敖理统计 二、离散型随机变量的边缘分布律 定义 设二维离散型随机变量(X,Y)的联合分布 律为 P{X=x,Y=yj}=P,i,j=1,2,. 记 p.=∑P=P{X=x,i=1,2, i=1 p.,=∑Pg=PW=y,j=1,2, 分别称p.(i=1,2,)和p(j=1,2,)为(X,Y) 关于X和关于Y的边缘分布律
1 1 ( , ) { , } , , 1,2, . { }, 1,2, , { }, 1,2, , ( 1,2, ) ( 1,2, ) ( , ) . i j ij i ij i j j ij j i i j X Y P X x Y y p i j p p P X x i p p P Y y j p i p j X Y X Y 设二维离散型随机变量 的联合分布 律为 记 分别称 和 为 关于 和关于 的边缘分布律 定义 二、离散型随机变量的边缘分布律

概率论与数理统外「 X2 Xi P21 Pa y2 P22 Pi2 P2j P P(X=x} Pi. PX=x}-PX=I=y}2D,=A
X Y x x x 1 2 i 12j yyy p p p 11 21 1i p p p 12 22 2i p p p 1 2 j j ij { } P X x i 1 P X x { } 1 1 { , }j j P X x Y y +++= 1 p 1 1 j j p 1 p +

X 概率论与敖理统计 x2 Xi P11 Pa P12 Pi y P P(X=x} P PX=,-2PX=Y=8,=p
X Y x x x 1 2 i 12j yyy p p p 11 21 1i p p p 12 22 2i p p p 1 2 j j ij { } P X x i 2 P X x { } 2 1 { , }j j P X x Y y 1 p 2 1 j j p 2 p ++++= 2 p

概率伦与教理统针」 x1 X2 P11 P21 P12 P22 Pui Pzi P(X=x} P1. P2. Pi. PX=}PW=,V-}2,-A
X Y x x x 1 2 i 12j yyy p p p 11 21 1i p p p 12 22 2i p p p 1 2 j j ij { } P X x i { } P X x i 1 { , } i j j P X x Y y 1 p 1 ij j p i p ++++= 2 p i p

概率论与敖理统计 X1 X2 Xi Pu P21 Pa Y2 P12 P22 Pn 三 Yj Puj p2i Pi P(X=x} P1。P2 P X x1X2.七 Pk P1.P2.P
X Y x x x 1 2 i 1 2 j y y y p p p 11 21 1i p p p 12 22 2i p p p 1 2 j j ij 1 p 2 p i p X k p 1 x 1 p 2 p i p 2 x i x { } P X x i

x2 P P11+P21+.+P1+ y2 P12 P22 Pi2 Pj p2i Pi P(X=x} P1. P2. P。 -Dn=pa
X Y x x x 1 2 i 1 2 j y y y p p p 11 21 1i p p p 12 22 2i p p p 1 2 j j ij 1 p 2 p i p { } P X x i { } P Y y j 1 P Y y { } 1 1 { , } i i P X x Y y 1 1 i i p 1 p + + + + = 1 p
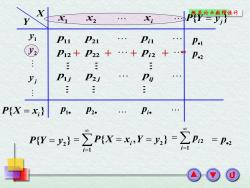
X2 c P P21 Pa P. P12+P22+ .+P2+ p.2 yj Puj Pzj P可 P(X=x} P1。 P2. PW=}=∑PX=x,Y=y}=∑P:=p i-1 ④
X Y x x x 1 2 i 1 2 j y y y p p p 11 21 1i p p p 12 22 2i p p p 1 2 j j ij 1 p 2 p i p { } P X x i { } P Y y j 2 P Y y { } 2 1 { , } i i P X x Y y 2 1 i i p 2 p + + + + = 1 p 2 p
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《概率论与数理统计》课程教学课件(PPT讲稿)第03章 多维随机变量及其分布 3.3 条件分布.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第03章 多维随机变量及其分布 3.4 相互独立的随机变量.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第03章 多维随机变量及其分布 3.5 两个随机变量的函数的分布.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第02章 随机变量及其分布 2.1 随机变量.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第02章 随机变量及其分布 2.2 离散型随机变量及其分布律.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第02章 随机变量及其分布 2.3 随机变量的分布函数.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第02章 随机变量及其分布 2.4 连续型随机变量及其概率密度.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第02章 随机变量及其分布 2.5 随机变量的函数的分布.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第01章 随机事件及其概率 1.1 随机试验.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第01章 随机事件及其概率 1.2 样本空间、随机事件.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第01章 随机事件及其概率 1.3 频率与概率.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第01章 随机事件及其概率 1.4 古典概型.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第01章 随机事件及其概率 1.5 条件概率、全概率公式与贝叶斯公式.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第01章 随机事件及其概率 1.6 独立性.pdf
- 《概率论与数理统计》课程教学课件(习题课,PPT)第一章 概率论的基本概念.ppt
- 《概率论与数理统计》课程教学资源(复习课PPT)第一章 概率论的基本概念 第二章 随机变量及其分布.ppt
- 《概率论与数理统计》课程教学资源(复习课PPT)第三章 多维随机变量及其分布 第四章 随机变量的数字特征 第五章 大数定律及中心极限定理.ppt
- 《概率论与数理统计》课程教学资源(复习课PPT)第六章 样本及抽样分布 第七章 参数估计 第八章 假设检验.ppt
- 山东理工大学:《概率论与数理统计》课程教学资源(试卷资料)试卷2_2018年11月概率D答案.pdf
- 山东理工大学:《概率论与数理统计》课程教学资源(试卷资料)试卷2_2018年11月概率D试卷.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第03章 多维随机变量及其分布 3.1 二维随机变量.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第04章 随机变量的数字特征 4.4 矩、协方差矩阵.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第04章 随机变量的数字特征 4.3 协方差及相关系数.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第04章 随机变量的数字特征 4.2 方差.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第04章 随机变量的数字特征 4.1 数学期望.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第05章 大数定律及中心极限定理 5.2 中心极限定理.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第05章 大数定律及中心极限定理 5.1 大数定律.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第06章 样本及抽样分布 6.3 统计量及其分布.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第06章 样本及抽样分布 6.1 总体与随机样本.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第07章 参数估计 7.7 单侧置信区间.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第07章 参数估计 7.5 正态总体均值与方差的区间估计.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第07章 参数估计 7.4 区间估计.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第07章 参数估计 7.3 估计量的评选标准.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第07章 参数估计 7.1 点估计.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第08章 假设检验 8.3 正态总体方差的假设检验.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第08章 假设检验 8.2 正态总体均值的假设检验.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第08章 假设检验 8.1 假设检验.pdf
- 《概率论与数理统计》课程教学资源(PPT课件)第1章 概率论的基本概念 第五节条件概率.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第1章 概率论的基本概念 第四节 等可能概型.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第1章 概率论的基本概念 第三节频率与概率.ppt
