《概率论与数理统计》课程教学课件（PPT讲稿）第04章 随机变量的数字特征 4.1 数学期望

概率论与敖理统外 4.1 随机变量的数学期望 数学期望的概念 二 数学期望的性质 三、小结

一、 数学期望的概念 二、 数学期望的性质 三、 小结 4.1 随机变量的数学期望

概率论与散理统外 一、数学期望的概念 引例1分赌本问题（产生背景） A、B两人赌技相同，各出 赌金100元，并约定先胜三局者为 胜，取得全部200元.由于出现意 外情况，在A胜2局B胜1局时， 不得不终止赌博，如果要分赌金， 该如何分配才算公平？

引例1 分赌本问题(产生背景) A、B 两人赌技相同, 各出 赌金100元,并约定先胜三局者为 胜, 取得全部 200 元.由于出现意 外情况 ,在 A 胜 2 局 B 胜1 局时, 不得不终止赌博, 如果要分赌金, 该如何分配才算公平? 一、 数学期望的概念

概率论与散理统计 分析假设继续赌两局，则结果有以下四种情况： AA AB BA BB A胜B负 A胜B负 B胜A负 B胜A负 A胜B负 B胜A负 A胜B负 B胜A负 把已赌过的三局(A胜2局B胜1局)与上述结果 相结合，即A、B赌完五局， 前三局： A胜2局B胜1局 后二局： AA AB BA BB A胜 B胜

前三局: A胜2局B胜1局 后二局: 把已赌过的三局(A 胜2局B 胜1局)与上述结果 相结合, 即A、B赌完五局, A A A B B A B B A胜 B胜 分析 假设继续赌两局,则结果有以下四种情况: A A A B B A B B A胜B负 A胜B负 A胜B负 B胜A负 B胜A负 A胜B负 B胜A负 B胜A负

概率轮与数理统外】 故有，在赌技相同的情况下，A、B最终获胜的 可能性大小之比为3：1， 即A应获得赌金的 而B只能获得赌金的4 因此，A能“期望”得到的数目应为 20×3+0×1-150(元. 44 而B能“期望”得到的数目，则为 20×+0=50w元

因此, A 能“期望”得到的数目应为 4 1 0 4 3 200    150(元), 而B 能“期望”得到的数目, 则为 4 3 0 4 1 200    50(元). 故有,在赌技相同的情况下, A、B最终获胜的 可能性大小之比为 3 :1, 即A 应获得赌金的 , 而 B 只能获得赌金的 4 3 . 4 1

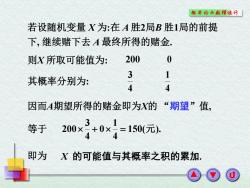
概率论与敖理统计 若设随机变量X为：在A胜2局B胜1局的前提 下，继续赌下去A最终所得的赌金. 则X所取可能值为： 200 0 3 1 其概率分别为： 4 4 因而A期望所得的赌金即为X的“期望”值， 等于 2×+0×10元 即为X的可能值与其概率之积的累加

因而A期望所得的赌金即为X的 “期望”值, 等于 X 的可能值与其概率之积的累加. 150( ). 4 1 0 4 3 200    元 即为 若设随机变量 X 为:在 A 胜2局B 胜1局的前提 下, 继续赌下去 A 最终所得的赌金. 则X 所取可能值为: 200 0 其概率分别为: 4 3 4 1

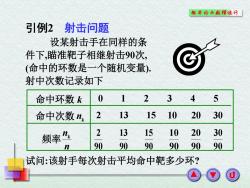
概率论与散理统外「 引例2射击问题 设某射击手在同样的条 件下，瞄准靶子相继射击90次， (命中的环数是一个随机变量) 射中次数记录如下 命中环数k 0 1 2 3 4 5 命中次数n 2 13 1510 20 30 频率 2 131510 2030 n 90 90 9090 90 90 试问：该射手每次射击平均命中靶多少环？

设某射击手在同样的条 件下,瞄准靶子相继射击90次, (命中的环数是一个随机变量). 射中次数记录如下 引例2 射击问题 试问:该射手每次射击平均命中靶多少环? 0 1 2 3 4 5 2 13 15 10 20 30 90 15 90 13 90 2 90 20 90 10 90 30 命中环数 k 命中次数 频率 nk n nk

概率论与散理统计 解平均射中环数= 射中靶的总环数 射击次数 0×2+1×13+2×15+3×10+4×20+5×30 90 2 13,15 =0× +1× +2×+3× 10 20 +4× 9090 90 90 90 30 +5x 90 =∑k k=3.37. n 设射手命中的环数为随机变量Y

解 平均射中环数 射击次数 射中靶的总环数  90 0 2  113  215  310  4 20  5 30  90 30 5 90 20 4 90 10 3 90 15 2 90 13 1 90 2 0               3.37.    5 k 0 k n n k 设射手命中的环数为随机变量 Y

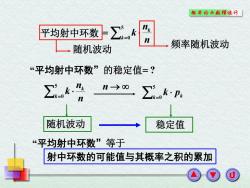
概率论与散理统外「 平均射中环数 ∑k 41 一随机波动 频率随机波动 “平均射中环数”的稳定值=？ ∑k n-→o0 ∑kp: 随机波动 稳定值 “平均射中环数”等于 射中环数的可能值与其概率之积的累加

    5 k 0 k n n 平均射中环数 k 频率随机波动 随机波动    5 k 0 k n n k n      5 k 0 k pk 随机波动 稳定值 “平均射中环数”的稳定值  ? “平均射中环数”等于 射中环数的可能值与其概率之积的累加

概率论与敖理统计 1、离散型随机变量的数学期望 定义设离散型随机变量X的分布律为 P{X=Xx}=Pk,k=1,2,. 若级数∑xP:绝对收敛，则称级数∑1P k=1 的和为随机变量X的数学期望，记为E(X).即 E(X)=∑xP k-1

1、 离散型随机变量的数学期望 定义 1 1 1 { } , 1,2, . , , ( ). ( ) . k k k k k k k k k k k X P X x p k x p x p X E X E X x p              设离散型随机变量 的分布律为 若级数 绝对收敛 则称级数 的和为随机变量 的数学期望 记为 即

概率论与散理统外「 分赌本问题 A期望所得的赌金即为X的数学期望 3。 B(X0=200×+0×4150(元. 41 射击问题 “平均射中环数”应为随机变量Y的数学期 望 E(Y)= 0×P0+1×P1+2×P2+3×P3+4×P4+5×P5:

分赌本问题 A 期望所得的赌金即为 X 的数学期望 射击问题 “平均射中环数”应为随机变量Y 的数学期 望 0 1 2 3 4 5 . ( ) p0 p1 p2 p3 p4 p5 E Y             150( ). 4 1 0 4 3 E(X)  200    元