《概率论与数理统计》课程教学课件（PPT讲稿）第06章 样本及抽样分布 6.1 总体与随机样本

概率论与散理统外 第一节 随机样本 一、总体与个体 二、随机样本的定义 三、小结

第一节 随机样本 一、总体与个体 二、随机样本的定义 三、小结

概率论与敖理统外 一、总体与个体 1.总体 试验的全部可能的观察值称为总体. 2.个体总体中的每个可能观察值称之， 实例1在研究2000名学生的 年龄时，这些学生的年龄的全 体就构成一个总体，每个学生 的年龄就是个体

一、总体与个体 1. 总体 试验的全部可能的观察值称为总体. 在研究2000名学生的 年龄时, 这些学生的年龄的全 体就构成一个总体, 每个学生 的年龄就是个体. 2. 个体 总体中的每个可能观察值称之. 实例1

概率论与数理统外 3.有限总体和无限总体 实例2考察这2000名学生的年龄，所得总体就 是有限总体，而测量某一湖泊任一点的深度， 所得总体就是无限总体 当有限总体包含的个体的 总数很大时，可近似地将它看 成是无限总体

考察这2000名学生的年龄，所得总体就 是有限总体，而测量某一湖泊任一点的深度， 所得总体就是无限总体. 3. 有限总体和无限总体 实例2 当有限总体包含的个体的 总数很大时, 可近似地将它看 成是无限总体

概率论与敖理统外 4.总体分布 实例3 在2000名大学一年级学生的年龄中， 年龄指标值为“15”、“16”、“17”、 “18”、“19”、“20”的依次有9、21、 132、1207、588、43名，它们在总体中所占比 率依次为 9 21 132 1207 588 43 2000'2000’2000 2000 2000’2000 即学生年龄的取值有一定的分布

4. 总体分布 在2000名大学一年级学生的年龄中, 年龄指标值为“15”、“16”、“17”、 “18”、“19”、“20”的依次有9、21、 132、1207、588、43名, 它们在总体中所占比 率依次为 实例3 , 2000 9 , 2000 21 , 2000 132 , 2000 1207 , 2000 588 , 2000 43 即学生年龄的取值有一定的分布

概率论与数理统外「 般地，我们所研究的总体，即研究对象的某 项数量指标X,其取值在客观上有一定的分布，X 是一个随机变量 总体分布的定义 我们把数量指标取不同数值的比率叫做总体分布. 如实例3中，总体就是数集{15,16,17,18,19,20}： 总体分布为 年龄15 16 17 18 19 20 9 21 132 1207 588 比率 43 2000 2000 2000 2000 2000 2000

一般地, 我们所研究的总体, 即研究对象的某 项数量指标 X , 其取值在客观上有一定的分布, X 是一个随机变量. 总体分布的定义 我们把数量指标取不同数值的比率叫做总体分布. 如实例3中, 总体就是数集 {15, 16, 17, 18, 19, 20}. 总体分布为 2000 43 2000 588 2000 1207 2000 132 2000 21 2000 9 15 16 17 18 19 20 比 率 年 龄

概率论与敖理统外 在数理统计中，人们都是通过从总体中抽取一部 分个体，根据获得的数据来对总体分布作出推断 的。被抽出的部分个体叫做总体的一个样本。 ·从总体抽取一个个体，就是对总体X进行一次观 察并记录其结果。我们在相同的条件下对总体X 进行n次重复的、独立的观察。将n次观察结果按 试验的次序记为X1,X2,Xm。由于X,X2,.,Xm 是对总体观察的结果，且各次观察是在相同的 条件下独立进行的，所以有理由认为X,X2,X。 是相互独立的，且与X具有相同分布的随机变量。 这样得到的X,X2,.,X称为来自于总体X的一个 简单随机样本，n称为这个样本的容量

• 在数理统计中，人们都是通过从总体中抽取一部 分个体，根据获得的数据来对总体分布作出推断 的。被抽出的部分个体叫做总体的一个样本。 • 从总体抽取一个个体，就是对总体X进行一次观 察并记录其结果。我们在相同的条件下对总体X 进行n次重复的、独立的观察。将n次观察结果按 试验的次序记为 。由于 是对总体X观察的结果，且各次观察是在相同的 条件下独立进行的，所以有理由认为 是相互独立的，且与X具有相同分布的随机变量。 这样得到的 称为来自于总体X的一个 简单随机样本，n称为这个样本的容量。 1 2 , , , X X X n 1 2 , , , X X X n 1 2 , , , X X X n 1 2 , , , X X X n

概率论与数理统外 如例3中，我们抽取一个容量为10的样本，记为 X1,X2,X1或(X1,X2,X10) X,表示这个样本中的第一个个体，是对总体的第 一次观察的结果，是一个随机变量，和总体X同一 分布： X 15 16 17 18 19 20 9 21 132 1207 588 43 Pk 2000 2000 2000 2000 2000 2000 X,表示这个样本中的第二个个体，是对总体的第 二次观察的结果，是一个随机变量， 和总体同 分布：

如例3中，我们抽取一个容量为10的样本，记为 1 2 10 1 2 10 X X X X X X , , , ( , , , ) 或 表示这个样本中的第一个个体，是对总体的第 一次观察的结果，是一个随机变量，和总体X同一 分布: X1 1 15 16 17 18 19 20 9 21 132 1207 588 43 2000 2000 2000 2000 2000 2000 k X p 表示这个样本中的第二个个体，是对总体的第 二次观察的结果，是一个随机变量，和总体X同一 分布: X2

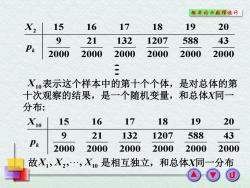
概率论与赦理统计 X2 15 16 17 18 19 20 9 21 132 1207 588 43 Pk 2000 2000 2000 2000 2000 2000 三 X表示这个样本中的第十个个体，是对总体的第 十次观察的结果，是一个随机变量，和总体X同 一 分布： X10 15 16 17 18 19 20 9 21 132 1207 588 43 Pk 2000 2000 2000 2000 2000 2000 故X1,X2,X0是相互独立，和总体X同一分布

2 15 16 17 18 19 20 9 21 132 1207 588 43 2000 2000 2000 2000 2000 2000 k X p 表示这个样本中的第十个个体，是对总体的第 十次观察的结果，是一个随机变量，和总体X同一 分布: X10 10 15 16 17 18 19 20 9 21 132 1207 588 43 2000 2000 2000 2000 2000 2000 k X p 1 2 10 故 X X X , , , 是相互独立，和总体X同一分布

概率论与散理统外 二、随机样本的定义 1.样本的定义 设X是具有分布函数F的随机变量，若X, X2,X,n是具有同一分布函数F、相互独立的 随机变量，则称X,X2,Xn为从分布函数F (或总体F、或总体X)得到的容量为n的简单 随机样本，简称样本 它们的观察值x,x2,x称为样本值，又称为 X的n个独立的观察值

二、随机样本的定义 1. 样本的定义 1 2 1 2 , , , , , , , , ( ) , . n n X F X X X F X X X F F X n 设 是具有分布函数 的随机变量 若 是具有同一分布函数 、相互独立的 随机变量 则称 为从分布函数 或总体 、或总体 得到的容量为 的简单 随机样本 简称样本 1 2 , , , , . n x x x X n 它们的观察值 称为样 又称为 的 个独 本 立的观察值 值

概率论与散理统计 2.简单随机抽样的定义 获得简单随机样本的抽样方法称为简单随机抽样. 根据定义得：若X,X2,Xn为F的一个样本， 则X1,X2,X的联合分布函数为 F*(x,x,x)=ΠF() i=1 又若X具有概率密度f, 则X1,X2,Xn的联合概率密度为 f*(x,x2,x)=Πf(x)

2. 简单随机抽样的定义 获得简单随机样本的抽样方法称为简单随机抽样. 根据定义得: 1 2 , , , , 若X X X F n 为 的一个样本 1 2 , , , 则X X X n 的联合分布函数为 1 2 1 *( , , , ) ( ). n n i i F x x x F x   又若 X 具有概率密度 f , 1 2 , , , 则X X X n 的联合概率密度为 1 2 1 *( , , , ) ( ). n n i i f x x x f x  