《概率论与数理统计》课程教学课件（PPT讲稿）第08章 假设检验 8.3 正态总体方差的假设检验

概率论与敖理统外 第三节正态总体方差的假设检验 一、单个总体的情况 二、两个总体的情况 三、小结

第三节 正态总体方差的假设检验 一、单个总体的情况 二、两个总体的情况 三、小结

概率论与数理统外 一、单个总体N(,o)的情况 设总体X~N(4,o2)4,o2均为未知， X,X2,Xn为来自总体X的样本 ()要求检验假设：H:o2=o,H1:σ2≠o2, 2 其中o,为已知常数设显著水平为a, 由于S2是σ2的无偏估计，当H,为真时， 比值。在附近摆动，不应过分大于或过分小于1， 60

一、单个总体 N(, 2 ) 的情况 ~ ( , ), , , 设总体 X N   2   2均为未知 : , : , 2 0 2 1 2 0 2 (1) 要求检验假设: H0   H    , 1 2 , , , X X X X n 为来自总体 的样本 . 其中 0 为已知常数 , 由于 S 2 是 2的无偏估计 , 当H0 为真时 1 , 1 1, 2 0 2 比 值 在 附近摆动 不应过分大于 或过分小于  s 设显著水平为

概率纶与散理统计 根据第六章§3，当H,为真时，n-1S 6 ~x2(n-10, 取X-n=s 作为统计量， 2 拒绝域的形式-≤人，或a- 2八≥k2, 此处k和k,的值由下式确定： P{H,为真拒绝H} -ea小小-a

根据第六章§3, ~ ( 1), ( 1) , 2 2 0 2 0   n n S H   当 为真时 , ( 1) 2 0 2 取 2 作为统计量   n  S  , ( 1) ( 1) 2 2 0 2 2 1 0 2 k n s k n s       拒绝域的形式 或 : 此处k1和k2的值由下式确定 { } P H0 为真拒绝H0 . ( 1) ( 1) 2 2 0 2 2 1 0 2 2 0                                 k n S k n S P 

概率轮与数理统外】 为了计算方便，习惯上取 %}号m小号 故得k1=X2a2(n-1),k2=X2/2(n-1) 拒绝域为： m=sxm-或w- ≥2(n-). 2 00 指它们的和集

指它们的和集 为了计算方便, 习惯上取 , 2 ( 1) 2 1 0 2 2 0             k n S P , 2 ( 1) 2 2 0 2 2 0             k n S P ( 1), ( 1). 2 2 / 2 2 故得 k1  1 / 2 n  k   n  拒绝域为: ( 1) 2 0 2    n s ( 1) 2 1 / 2 n  ( 1) 2 0 2    n s 或 ( 1). 2   / 2 n 

概率论与敖理统外 (2)单边检验问题的拒绝域（设显著水平为a) 右边假设检验：H。:o2≤o2,H1:o2>o2, 因为H,中的全部σ2都比H1中的o2要小， 当H为真时，S2的观察值s2往往偏大， 拒绝域的形式为：s2≥k. 此处k的值由下式确定： PH,为真拒绝H}=PsS≥

(2)单边检验问题的拒绝域 (设显著水平为) : , : , 2 0 2 1 2 0 2 右边假设检验: H0   H   , 2 1 2 因为H0中的全部 都比 H 中的 要小 , , 2 2 当H1为真时 S 的观察值s 往往偏大 拒绝域的形式为: . 2 s  k 此处 k 的值由下式确定: { } P H0 为真拒绝H0 { } 2 2 0  P 2 S  k  

概率论与数理统外「 2 2 001 J(n-1)S2 (因为o2≤o,2) 要使P{H,为真拒绝H}≤a, 只满令p:。-a 因为0s-xm-1所以axm-l 00

           ( 1) ( 1) 2 0 2 0 2 2 0 2     n S n k P ( ) ( 1) ( 1) 2 0 2 2 0 2 2 2 0 2                   因 为 n S n k P { } , 要使 P H0 为真拒绝H0  . ( 1) ( 1) 2 0 2 2 2 0 2                 n S n k 只需令 P ~ ( 1), ( 1) 2 2 2   n n S   因为 ~ ( 1), ( 1) 2 2 0   n n k    所以

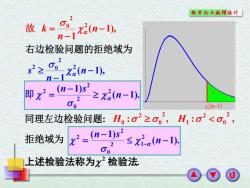
概率论与敖理统外 2 n1n-, 故k= 右边检验问题的拒绝域为 0 52≥ x2(n-1), 即-a2z- Xa(n-1) 同理左边检验问题：H,:σ2之o, 2 H1:σ2<o0, 拒绝域为 z2=" ≤a(n-1). 上述检验法称为x检验法

( 1), 1 2 2 0    n n k    故 ( 1), 1 2 2 2 0    n n s    右边检验问题的拒绝域为 ( 1). ( 1) 2 2 0 2 2     n n s    即 同理左边检验问题: : , : , 2 0 2 1 2 0 2 H0   H   拒绝域为 ( 1). ( 1) 2 2 1 0 2 2      n n s     . 上述检验法称为 2 检验法

概率论与散理统外「 例1某厂生产的某种型号的电池，其寿命长期以 来服从方差σ2=5000（小时2）的正态分布，现有一 批这种电池，从它生产情况来看，寿命的波动性有 所变化.现随机的取26只电池，测出其寿命的样本 方差s2=9200(小时2).问根据这一数据能否推断这 批电池的寿命的波动性较以往的有显著的变化？ (a=0.02) 解要检验假设H:o2=5000,H1:o2≠5000， n=26,a=0.02,o,2=5000, xa/2(n-1)=x.01(25)=44.314

(  0.02) 解 : 5000, : 5000, 2 1 2 要检验假设 H0   H   n  26,   0.02, 5000, 2  0  ( 1) (25) 44.314, 2 0.01 2   / 2 n     例1 某厂生产的某种型号的电池, 其寿命长期以 来服从方差 =5000 (小时2 ) 的正态分布, 现有一 批这种电池, 从它生产情况来看, 寿命的波动性有 所变化. 现随机的取26只电池, 测出其寿命的样本 方差s 2=9200(小时2 ). 问根据这一数据能否推断这 批电池的寿命的波动性较以往的有显著的变化? 2 

概率论与敖理统计 a2(n-1)）=2X6(25)=11.524, 拒绝域为：a-≤11524，或-0 ≥44.314. 60 00 因为n-1s2 25×9200 2 5000 =46>44.314, 所以拒绝Ho, 认为这批电池的寿命的波动性较以往的有 显著的变化

( 1) (25) 11.524, 2 0.99 2 1 / 2 n     ( 1) 2 0 2    n s 拒绝域为: 11.524, ( 1) 2 0 2    n s 或 44.314 . 46 5000 ( 1) 25 9200 2 0 2      n s 因为  44.314 , , 所以拒绝H0 认为这批电池的寿命的波动性较以往的有 显著的变化

概率论与数理统外 例2某自动车床生产的产品尺寸服从正态分布， 按规定产品尺寸的方差o不得超过0.1，为检验 该自动车床的工作精度，随机的取25件产品，测 得样本方差2=0.1975.问该车床生产的产品是 否达到所要求的精度？(a=0.05) 解要检验假设H:o2≤0.1，H1:o2>0.1, n=25,2x6.5(24)=36.415, 因为n-1)s2_24×0.1975 2 0.1 47.4>36.415, 所以拒绝Ho, 认为该车床生产的产品没有达到所要求的精度：

解 : 0.1, : 0.1, 2 1 2 要检验假设 H0   H   n  25, (24) 36.415, 2  0.05  47.4 0.1 ( 1) 24 0.1975 2 0 2      n s 因为  36.415, , 所以拒绝H0 认为该车床生产的产品没有达到所要求的精度. 例2 某自动车床生产的产品尺寸服从正态分布, 按规定产品尺寸的方差 不得超过0.1, 为检验 该自动车床的工作精度, 随机的取25件产品, 测 得样本方差s 2=0.1975. 问该车床生产的产品是 否达到所要求的精度? 2  (  0.05)