《概率论与数理统计》课程教学课件(PPT讲稿)第07章 参数估计 7.7 单侧置信区间

概率论与敖理统外 第七节 单侧置信区间 一、问题的引入 二、基本概念 三、典型例题 四、小结
第七节 单侧置信区间 二、基本概念 三、典型例题 一、问题的引入 四、小结

概率论与数理统外 一、问题的引入 在以上各节的讨论中对于未知参数0,我们给 出两个统计量8,0,得到的双侧置信区间(日,0). 但在某些实际问题中,例如,对于设备、元 件的寿命来说,平均寿命长是我们希望的,我们 关心的是平均寿命0的“下限”;与之相反,在 考虑产品的废品率p时,我们常关心参数p的 “上限”,这就引出了单侧置信区间的概念
一、问题的引入 , , ( , ). , , 出两个统计量 得 到 的双侧置信区间 在以上各节的讨论中对于未知参数 我们给 但在某些实际问题中, 例如, 对于设备、元 件的寿命来说, 平均寿命长是我们希望的, 我们 关心的是平均寿命 的“下限”; 与之相反, 在 考虑产品的废品率 p时, 我们常关心参数 p的 “上限”, 这就引出了单侧置信区间的概念.

概率论与敖理统计 二、基本概念 1.单侧置信区间的定义 对于给定值au(00≥1-a, 则称随机区间(0,o)是0的置信水平为1-a的单 侧置信区间,0称为0的置信水平为1-a的单侧置 信下限
二、基本概念 1. 单侧置信区间的定义 1 2 1 2 (0 1), , , , ( , , , ) , { } 1 , n n X X X X X X P 对于给定值 若由样本 确定的统计量 对于任意 满足 ( , ) 1 , 1 . 则称随机区间 是 的置信水平为 的单 侧置信区间 称为 的置信水平为 的单侧置 信下限

概率论与数理统外「 又如果统计量0=0X,X2,.,X,),对于任 意0e⊙满足 P{0<0≥1-a, 则称随机区间(-∞,0)是0的置信水平为1-a的 单侧置信区间,0称为0的置信水平为1-o的单侧 置信上限
1 2 ( , , , ), { } 1 , X X X n P 又如果统计量 对于任 意 满足 ( , ) 1 , 1 . 则称随机区间 是 的置信水平为 的 单侧置信区间 称为 的置信水平为 的单侧 置信上限

概率论与敖理统外 2.正态总体均值与方差的单侧置信区间 设正态总体X的均值是4,方差是σ2,(均为未知 X,X,水是一个样本由 SI 'tn-1 有p-a-0}-1-a
2. 正态总体均值与方差的单侧置信区间 , ,( ) 设正态总体 X 的均值是 方差是 2 均为未知 , , , , X1 X2 Xn 是一个样本 ~ ( 1), / t n S n X 由 ( 1) 1 , / t n S n X 有 P ( 1) 1 , t n n S 即 P X

概率论与数理统外 于是得的一个置信度为1一α的单侧置信区间 (-m-小 的置信度为1-a的置信下限μ=X-S (n-1) 又根器。-x- 有P>左a-1-a
( 1), , t n n S X 的置信度为1的置信下限 t (n 1). n S X ~ ( 1), ( 1) 2 2 2 n n S 又根据 ( 1) 1 , ( 1) 2 2 1 2 n n S 有 P 于是得的一个置信度为1的单侧置信区间

概率论与敖理统计 于是得σ的一个置信度为1-o的单侧置信区间 (n-1)S2) xic(n-1) o的置信度为1-a的单侧置信上限 o2=n-1)S2 ia(n-1))
1 于是得 2的一个置信度为 的单侧置信区间 , ( 1) ( 1) 0, 2 1 2 n n S 1 2的置信度为 的单侧置信上限 . ( 1) ( 1) 2 1 2 2 n n S 1 , ( 1) ( 1) 2 1 2 2 n n S 即 P

概率论与散理统外 三、典型例题 例1设从一批灯泡中,随机地取5只作寿命试验, 测得寿命(以小时计)为1050,1100,1120,1250, 1280,设灯泡寿命服从正态分布,求灯泡寿命平均 值的置信度为0.95的单侧置信下限. 解1-au=0.95,n=5,x=1160,s2=9950, ta(n-1)=t.os(4)=2.1318, μ的置信度为0.95的置信下限 4=x-、.(n-1)=1065. Nn
三、典型例题 设从一批灯泡中, 随机地取5只作寿命试验, 测得寿命(以小时计)为1050, 1100, 1120, 1250, 1280, 设灯泡寿命服从正态分布, 求灯泡寿命平均 值的置信度为0.95的单侧置信下限. 解 1 0.95, n 5, x 1160, ( 1) (4) 2.1318, t n t 0.05 9950, 2 s 的置信度为0.95的置信下限 t (n 1) 1065. n s x 例1
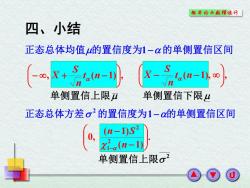
概率论与散理统计 四、小结 正态总体均值的置信度为1-oα的单侧置信区间 单侧置信上限π 单侧置信下限4 正态总体方差σ2的置信度为1-o的单侧置信区间 单侧置信上限。2
. ( 1) ( 1) 0, 2 1 2 n n S 四、小结 ( 1), , t n n S X 正态总体均值的置信度为1 的单侧置信区间 1 正态总体方差 2 的置信度为 的单侧置信区间 , ( 1), t n n S X 单侧置信上限 单侧置信下限 2 单侧置信上限
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《概率论与数理统计》课程教学课件(PPT讲稿)第06章 样本及抽样分布 6.1 总体与随机样本.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第06章 样本及抽样分布 6.3 统计量及其分布.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第05章 大数定律及中心极限定理 5.1 大数定律.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第05章 大数定律及中心极限定理 5.2 中心极限定理.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第04章 随机变量的数字特征 4.1 数学期望.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第04章 随机变量的数字特征 4.2 方差.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第04章 随机变量的数字特征 4.3 协方差及相关系数.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第04章 随机变量的数字特征 4.4 矩、协方差矩阵.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第03章 多维随机变量及其分布 3.1 二维随机变量.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第03章 多维随机变量及其分布 3.2 边缘分布.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第03章 多维随机变量及其分布 3.3 条件分布.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第03章 多维随机变量及其分布 3.4 相互独立的随机变量.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第03章 多维随机变量及其分布 3.5 两个随机变量的函数的分布.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第02章 随机变量及其分布 2.1 随机变量.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第02章 随机变量及其分布 2.2 离散型随机变量及其分布律.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第02章 随机变量及其分布 2.3 随机变量的分布函数.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第02章 随机变量及其分布 2.4 连续型随机变量及其概率密度.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第02章 随机变量及其分布 2.5 随机变量的函数的分布.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第01章 随机事件及其概率 1.1 随机试验.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第01章 随机事件及其概率 1.2 样本空间、随机事件.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第07章 参数估计 7.5 正态总体均值与方差的区间估计.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第07章 参数估计 7.4 区间估计.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第07章 参数估计 7.3 估计量的评选标准.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第07章 参数估计 7.1 点估计.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第08章 假设检验 8.3 正态总体方差的假设检验.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第08章 假设检验 8.2 正态总体均值的假设检验.pdf
- 《概率论与数理统计》课程教学课件(PPT讲稿)第08章 假设检验 8.1 假设检验.pdf
- 《概率论与数理统计》课程教学资源(PPT课件)第1章 概率论的基本概念 第五节条件概率.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第1章 概率论的基本概念 第四节 等可能概型.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第1章 概率论的基本概念 第三节频率与概率.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第1章 概率论的基本概念 第二节样本空间,随机事件.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第1章 概率论的基本概念 第一节随机试验.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第1章 概率论的基本概念_前言.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第2章 随机变量及其分布 第五节 随机变量的函数分布.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第2章 随机变量及其分布 第四节 连续型随机变量及其概率密度.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第2章 随机变量及其分布 第三节 随机变量的分布函数.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第2章 随机变量及其分布 第二节 离散型随机变量及其分布律.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第2章 随机变量及其分布 第一节随机变量.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第3章 多维随机变量及其分布 第五节 两个随机变量的函数分布.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第3章 多维随机变量及其分布 第四节 相互独立的随机变量.ppt
