《概率论与数理统计》课程教学资源（PPT课件）第2章 随机变量及其分布 第一节随机变量

第二章 随机变量及其分布 第一节 随机变量 一、随机变量的引入 二、随机变量的概念

二、随机变量的概念 一、随机变量的引入 第一节 随机变量 第二章 随机变量及其分布

一、随机变量的引入 1.为什么引入随机变量？ 概率论是从数量上来研究随机现象内在规律 性的，为了更方便有力地研究随机现象，就要用 数学分析的方法来研究，因此为了便于数学上的 推导和计算，就需将任意的随机事件数量化.当 把一些非数量表示的随机事件用数字来表示时， 就建立起了随机变量的概念

概率论是从数量上来研究随机现象内在规律 性的，为了更方便有力地研究随机现象，就要用 数学分析的方法来研究， 因此为了便于数学上的 推导和计算，就需将任意的随机事件数量化．当 把一些非数量表示的随机事件用数字来表示时， 就建立起了随机变量的概念． 1. 为什么引入随机变量? 一、随机变量的引入

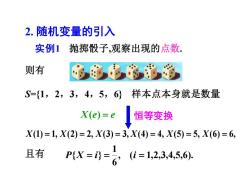
2.随机变量的引入 实例1抛掷骰子，观察出现的点数. 则有 S={1,2,3,4,5,6} 样本点本身就是数量 X(e)=e 恒等变换 X(1)=1,X(2)=2,X(3)=3,X(4)=4,X(⑤)=5，X(6)=6, 且有 x- (i=1,2,3,4,5,6)

实例1 抛掷骰子,观察出现的点数. X(1) = 1, X(2) = 2, X(3) = 3, X(4) = 4, X(5) = 5, X(6) = 6, , ( 1,2,3,4,5,6). 6 1 P{X = i} = i = S={1，2，3，4，5，6} 样本点本身就是数量 恒等变换 且有 X(e) = e 则有 2. 随机变量的引入

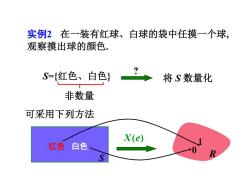
实例2在一装有红球、白球的袋中任摸一个球， 观察摸出球的颜色. S={红色、白色} 将S数量化 非数量 可采用下列方法 X(e) 红色 白色

实例2 在一装有红球、白球的袋中任摸一个球, 观察摸出球的颜色. S={红色、白色} 非数量 将 S 数量化 ? 可采用下列方法 S 红色 白色 X(e) R 1 0

即有 X(红色)=1，X(白色)=0 4 e)={ ，e=白色. 这样便将非数量的S={红色，白色}数量化了

即有 X (红色)=1 ,    = = = 0, . 1, , ( ) 白色 红色 e e X e X (白色)=0. 这样便将非数量的 S={红色，白色} 数量化了

二、随机变量的概念 1.定义 设E是随机试验，它的样本空间是S={}.如 果对于每一个e∈S,有一个实数X(e)与之对应， 这样就得到一个定义在S上的单值实值函数X(e), 称X(e)为随机变量

( ) . ( ), , ( ) , , { }. 称 为随机变量 这样就得到一个定义在 上的单值实值函数 果对于每一个 有一个实数 与之对应 设 是随机试验 它的样本空间是 如 X e S X e e S X e E S e  = 二、随机变量的概念 1.定义

2.说明 (1)随机变量与普通的函数不同 随机变量是一个函数，但它与普通的函数有 着本质的差别，普通函数是定义在实数轴上的，而 随机变量是定义在样本空间上的（样本空间的元 素不一定是实数). (2)随机变量的取值具有一定的概率规律 随机变量随着试验的结果不同而取不同的值， 由于试验的各个结果的出现具有一定的概率，因 此随机变量的取值也有一定的概率规律

随机变量随着试验的结果不同而取不同的值, 由于试验的各个结果的出现具有一定的概率, 因 此随机变量的取值也有一定的概率规律. (2)随机变量的取值具有一定的概率规律 随机变量是一个函数 , 但它与普通的函数有 着本质的差别 ,普通函数是定义在实数轴上的,而 随机变量是定义在样本空间上的 (样本空间的元 素不一定是实数). 2.说明 (1)随机变量与普通的函数不同

3)随机变量与随机事件的关系 随机事件包容在随机变量这个范围更广的概 念之内.或者说：随机事件是从静态的观点来研究 随机现象，而随机变量则是从动态的观点来研究随 机现象

随机事件包容在随机变量这个范围更广的概 念之内.或者说 : 随机事件是从静态的观点来研究 随机现象,而随机变量则是从动态的观点来研究随 机现象. (3)随机变量与随机事件的关系

实例3 掷一个硬币，观察出现的面，共有两个 结果： e1=(反面朝上)， e2=(正面朝上)， 若用X表示掷一个硬币出现正面的次数，则有 e=(反面朝上) X(e) 0→Xe,)=0 e2=(正面朝上) 1→X(e2)=1 即X(e)是一个随机变量

实例3 掷一个硬币, 观察出现的面 , 共有两个 结果: ( ), e1 = 反面朝上 ( ), e2 = 正面朝上 若用 X 表示掷一个硬币出现正面的次数, 则有 X(e) ( ) e1 = 反面朝上 ( ) e2 = 正面朝上 1 0 → X(e1 ) = 0 → X(e2 ) = 1 即 X (e) 是一个随机变量

实例4设盒中有5个球(2白3黑)，从中任抽3个，则 X(e)=抽得的白球数， 是一个随机变量.且X(e)的所有可能取值为： 0,1,2. 实例5设某射手每次射击打中目标的概率是0.8， 现该射手射了30次，则 X(e)=射中目标的次数， 是一个随机变量.且X(e)的所有可能取值为： 0,1,2,3,30

实例4 设盒中有5个球 (2白3黑), 从中任抽3个,则 X(e) = 抽得的白球数, 是一个随机变量. 实例5 设某射手每次射击打中目标的概率是0.8, 现该射手射了30次, 则 X(e) = 射中目标的次数, 是一个随机变量. 且 X(e) 的所有可能取值为: 0, 1, 2. 且 X(e) 的所有可能取值为: 0, 1, 2, 3,  , 30