《概率论与数理统计》课程教学资源（复习课PPT）第六章 样本及抽样分布 第七章 参数估计 第八章 假设检验

能事伦与散理统计」 第六章数理统计的基本概念 创关键词： 总体 个体 样本 统计量 X2-分布 t-分布 下分布

第六章 数理统计的基本概念 关键词： 总 体 个 体 样 本 统 计 量 2  −分布 t −分布 F −分布

概華论与款醒硫外「 1.总体与样本 ·总体：研究对象的全体 ·抽样：从总体X中抽取有限个个体对总体进行 观察的取值过程。 ·随机样本：随机抽取的n个个体的集合 (X1,X2,.,X),n为样本容量 X以) 1.每个X与X同分布 4w) 2.X1,X2,.,Xn是相互独立的随机变量

1.总体与样本 • 总体：研究对象的全体 • 抽样：从总体X中抽取有限个个体对总体进行 观察的取值过程。 • 随机样本：随机抽取的n个个体的集合 (X1,X2,.,Xn), n为样本容量 1. 每个Xi与X同分布 2. X1,X2,.,Xn是相互独立的随机变量

概车纶与款理统外 2.抽样分布 ·统计量：样本的不含任何未知参数的函数。 ·常用统计量：设(X1,X2,.,X)为取自总体X的样本 1样本均值又=2名 2样本方老S-十2X-X.5为样本标准养 3.样本矩 4空r低2及56 阶中心矩：B=2(X-X(k=12,） 设X1,X2,X是总体X的样本，若E(X)=4,DX)=o2, X=4D五=g,S)=a

2.抽样分布 • 统计量：样本的不含任何未知参数的函数。 • 常用统计量：设（X1,X2,.,Xn）为取自总体X的样本 1 1 1. X n i i X n = 样本均值 =  2 2 1 1 2. ( ) , 1 n i i S X X S n = = − 样本方差 −  为样本标准差 ( ) ( ) 1 1 1 3. 1,2, 1 ( ) 1,2, n k k i i n k k i i k A X k n k B X X k n = = = = = − =   样本矩 阶矩： 阶中心矩： 2 2 2 2 2 , ,., ( ) , ( ) ( ) , ( ) , ( ) . X X X E X D X n E X D X E S n      = = = = = 设 1 X 是总体 的样本，若 ， 则

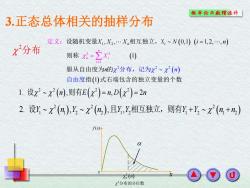
概率伦与款程统外 3.正态总体相关的抽样分布 定义：设随机变量X,X2,.Xn相互独立，X,~(0,1)(位=1,2，.，n) x分布 则称-立X () 服从自由度为n的x2分布，记为x2~x2(n) 自由度指()式右端包含的独立变量的个数 1.设x2~X2(n),则有E(x2)=n,D(x2)=2n 2.设r~X(n),出，~X(h),且X,相互独立，则有y+~X(n+n) f(x)4 xa(寸 x分布的分位数

3.正态总体相关的抽样分布 2  分布 ( ) ( ) ( ) ( ) ( ) 1 2 2 2 2 2 2 1 , , 0,1 1, 2, , 1 1 n i n i n i X X X N i X n n    n  =  = =   设随机变量 相互独立，X 则称 服从自由度为 的 ， 定 指 式右端包含 分布 记为 自 度 的独立变 义： 由 量的个数 ( ) ( ) ( ) 2 2 2 2 1. , , 2 设     = = n E n D n 则有 ( ) ( ) ( ) 2 2 2 1 1 2 2 1 2 1 2 1 2 2. , , , 设Y n Y n Y Y Y Y n n   +  +    且 相互独立，则有 ( ) 2 n  0 2  分布的分位数 x f x( ) 

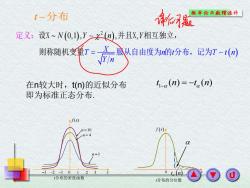
t-分布 概车纶与散理统外「 定义：设x~N(0,1),Y一(，并且X,Y相互独立， 则称随机变看T=X服从自由度为的分布，记为T-1(n) 在n较大时，t(n)的近似分布 t-a(n)=-ta (n) 即为标准正态分布！ (x) () -3-2-1012 o t (n 1分布的密度函数 分布的分位数

t −分布( ) ( ) ( ) 2 N Y n 0,1 , , , X T n t T t Y n Y n  = 设X  并且X 相互独立， 则称随机变量 服从自由度为 的 分布，记为 定义：  t n  ( ) f x( ) 0 x t分布的分位数 n =10 −3 1 3 x f x( ) n =1 n = 4 −2 −1 0 2 t分布的密度函数 1 t n t n ( ) ( ) 在n较大时，t(n)的近似分布 −  = − 即为标准正态分布

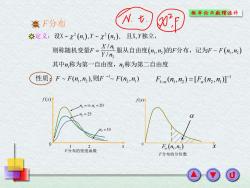
概率伦与款程统外 来F分布 N.七 #定义：设X~x2(n),Y~x2(n2),且X,Y独立， 则称随机变量F X1m服从自由度(n,n)的F分布，记为F-F(m,) YIn 其中n,称为第一自由度，n,称为第二自由度 性质 F~F(nn),F(nn) F-a(n,n2)=[E(n2,n)]f f(x) f(x) 乃=0,4=20 25 =10 0 Fa(n,n) F分布的密度函数 F分布的分位数

( ) ( ) ( ) ( ) 2 2 1 2 1 1 2 1 2 2 1 2 , , , / , , / n Y n Y X n F n n F F F n n Y n n n     = 设X 且X 独立， 则称随机变量 服 定义： 从自由度 的 分布，记为 其中 称为第一自由度， 称为第二自由度 F分布 1 F F n n F F n n ~ ( , ), ~ ( , ) 1 2 2 1 性质： 则 − 0 1 2 x f x( ) 2 1 n n =  = , 20 2 n = 25 2 n =10 F分布的密度函数 0 ( ) x 1 2 F n n,  f x( )  F分布的分位数 1 1 1 2 2 1 F n n F n n ( , ) [ ( , )]   − − =

正态总体样本均值和方差的分希 定理66：设(X,X,奶总体N(uo)的样本，S 分别是样本均值和样本方差，则有： 2 (n-1)s2 (n-1 灭nw(u,a) 3.灭和S相互独立 定理67：设(X,.,X是总体N(4,o2)的样本，x和S2分别是样本 均值和样本方差，则有：- SIn

正态总体样本均值和方差的分布 ( ) ( ) ( ) ( ) ( ) 2 2 2 1 2 2 2 2 2 , , , , , 1. X , - 1 2. 1 3. 6.6 n n X X X N X S N n S n X S         − 设 是总体 的样本， 分别是样本均值和样本方差 定理 ： ，则有： 和 相互独立 ( ) ( ) ( ) ( ) 2 2 1 . , , , 1 / 6 7 X X N S n X t n S n   −  − 设 是总体 的样本，X和 分别是样本 均值和样本方差，则有： 定理 ：

上述定理的常见形式： 概華论与款醒硫外「 X-u ≈N(0,1) X-4 ol/n SIn ~tn- x.-0a 1 i-1 XNW.6") X0必 Nwl)

~ (0,1) / N n X  −  ~ ( 1) / − − t n S n X  ( ) ~ ( ) 1 2 1 2 2 X n n i i    = − 上述定理的常见形式：

棍丰伦与散理统针」 例2：已知X,X2，Xn)来自正态总体X~N(1,2),X为样本均值，则 下列结论成立的是： 61 X-1 N(o,) n 2cx-心aw S2x-a wea

下列结论成立的是： 例2 :已知(X1 , X2 ,Xn )来自正态总体X ~ N(1,2 2 ), X为样本均值,则 ~ ( ) 2 / 1 t n n X A − ． ( 1) ~ ( ,1) 4 1 1 2 B X F n n i  i = ． − ( 1) ~ ( ) 4 1 2 1 2 C X n n i  i  = ． − ~ (0,1) 2 / 1 N n X D − ．

概率伦与款理统外 第七章参数估计 妙关键词： 矩估什法 极大似然估计法 置信区间 置信度

第七章 参数估计 关键词： 矩估计法 极大似然估计法 置信区间 置信度